Ex. 1: Surrogate Modeling¶
Let’s construct a 2D function \(r(x,y)\) that’s: linear in \(x\), cubic in \(y\), exponentially decays away from the origin and has a little noise to mimic realistic responses of a computational model. In the following example we’ll take our “model” to be the simple function defined by:
In the following steps, we’ll use nodeworks to sample a relevant \((x,y)\) space and construct a surrogate model from responses of the function \(r\) evaluated at the sample points.
Sampling¶
Following the steps below, we’ll create a simple factorial design for sampling the model:
Launch Nodeworks and right click on the empty sheet to bring up the menu. Scroll down to
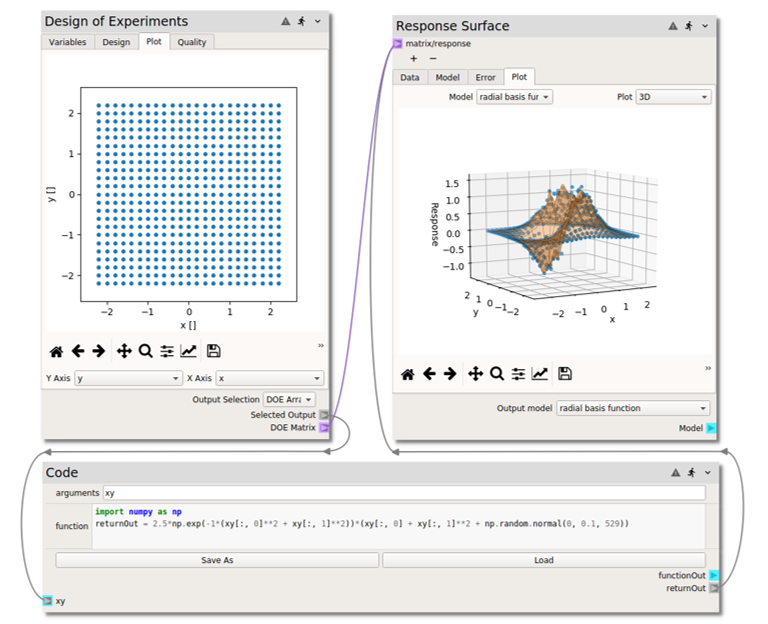
Add Node, then down to theSurrogate Modeling and Analysiscollection of nodes and (left) click onDesign of Experimentsto populate the sheet with the node.On the
Variablestab, click thebutton twice to initiate the \(x\) and \(y\) variables.
By selecting the default entries in thee table, set the
variablenames toxandyfor clarity. (The new entries default totypeDouble Precisionwithoutarg(s)orunitsandlinkNone, so no change is needed for these properties.)We’ll look at a phase space of \((x,y) \in [-2,2] \times [-2, 2]\) with a simple interval spacing of 0.2. In order to cover the edges of the domain of interest, set the
fromandtoof both variables to-2.2and2.2, respectively. (You can set thelevelsof each to23, but we’ll use the same interval for both \(x\) and \(y\), so variable specific levels won’t be necessary.Click over to the
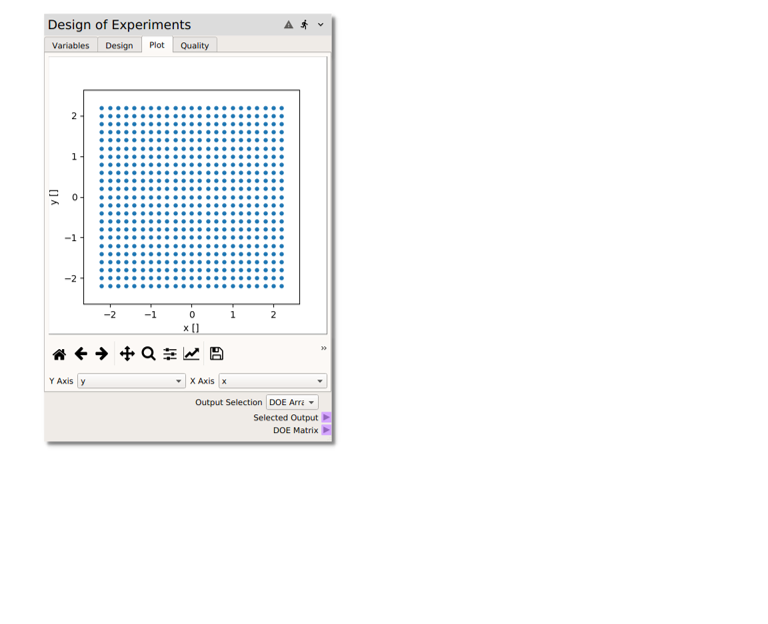
Designtab, set theMethodtofactorialand theLevelsto23and click on theBuildbutton to generate the sample. The uniformly spaced 2D factorial design can be viewed on thePlottab, as shown below.
Model Evaluation¶
Now we need to evaluate the model at the sampling points. In this case, we are using the simple function \(r\), which can be easily evaluated with a code node following the steps below:
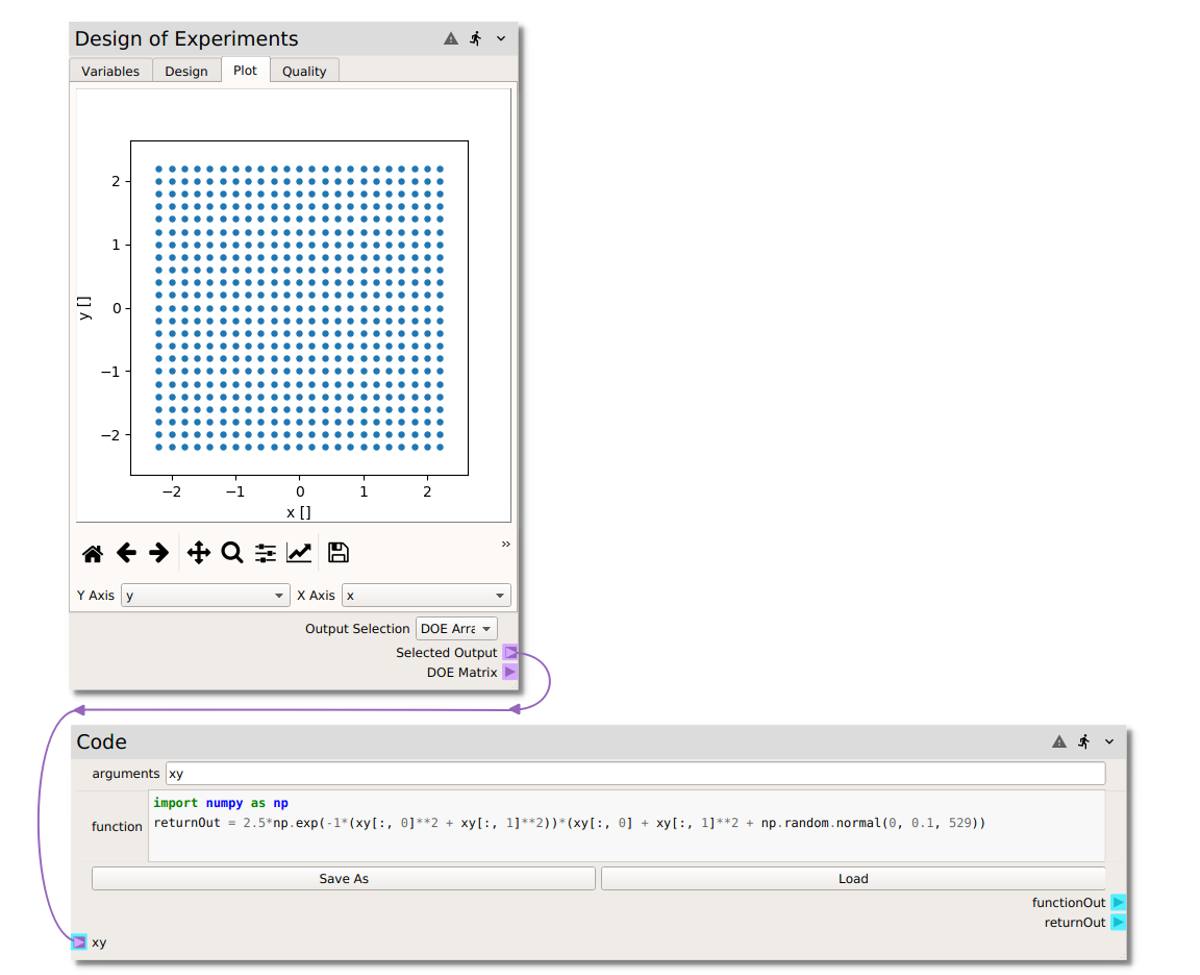
Right click or type to access the node menu and add a
Codenode.Set the arguments to
xy(since we will pass into the code node an array of the \((x,y)\) values at the 529 design points).Evaluate the model function \(r\) with a python code. Non-python users can simply copy and paste in the code below into the
functionentry.
import numpy as np
returnOut = 2.5*np.exp(-1*(xy[:, 0]**2 + xy[:, 1]**2))*(xy[:, 0] + xy[:, 1]**2 + np.random.normal(0, 0.1, 529))
Then
Set the
Output Selectionin the DOE node toDOE Array(our \((x,y)\) array).Add a connection from the
Selected Outputterminal to thexy
At this point, pressing will send the data from the DOE node to the code node for
evaluation. We could connect the code node output to a print node to verify that the
function was being evaluated correctly. However in this case (with a previously tested code),
we direct the code node output to an RSM node in the section below.
Surrogate Modeling¶
Now, we will take the function \(r\) evaluated at the \((x,y)\) sample points and construct a surrogate model, specifically a Gaussian response surface approximation of the “model” by following these steps:
Right click or type to access the node menu and add a
Response Surfacenode, found in theSurrogate Modeling and Analysisnode collectionConnect both the
DOE Matrixterminal of the DOE tab and thereturnOutterminal of the code node to thematrix/responseterminal of the RS node.Click on the
Modeltab of the RS node and check (under thefitcolumn of the table) theradial basis functionmodel. In the options set theepsilonvalue to 0.3. For now, theFunctionandSmoothfields can be left atmultiquadricand0, respectively.Now
the sheet. This will send the data from the DOE node to the code node, calculating the response of the “model” at the sample points, and from there onto the RSM node, constructing a Gaussian process surrogate model. The response data can be viewed in the
Datatab in raw table format and in thePlottab as a 3D surface with response data points from the “actual model” superimposed.
- Although we now have a surrogate model, we may want to know:
How good is this surrogate?
What is the error in the surrogate relative to the full model?
Could we build a better surrogate with different model settings a different model option?
We’ll explore these questions in the following section.
(Surrogate) Model Error¶
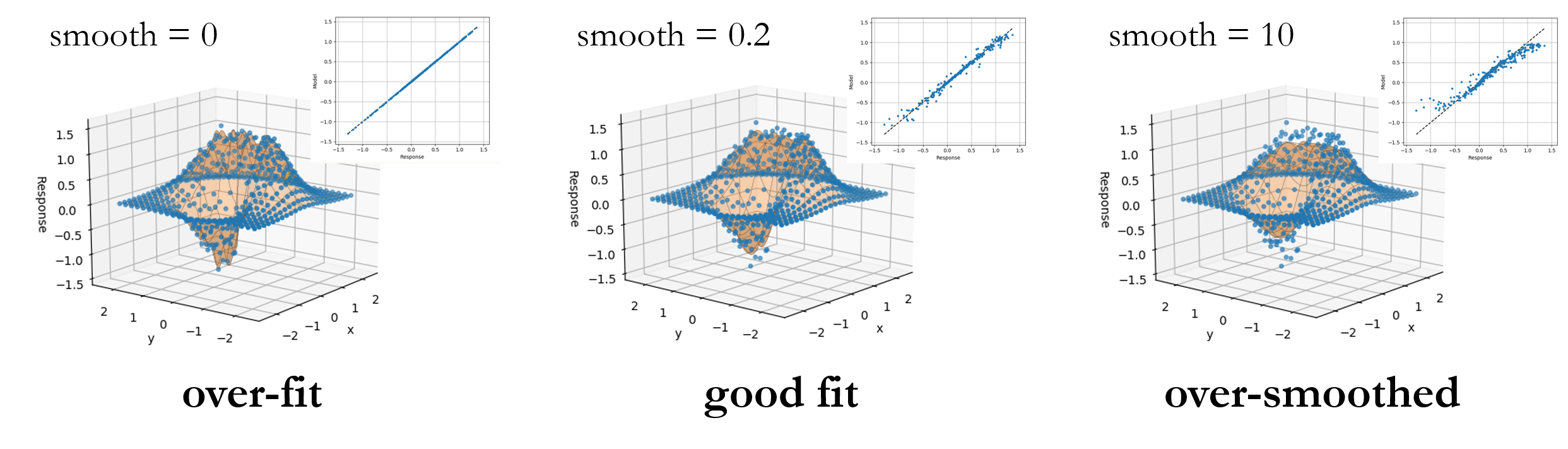
The surrogate constructed in the previous section used a multiquadric radial basis function
without smoothing, i.e., we left the Smooth parameter at the default 0 value. In this
case, the RBF is a pure interpolator. In other words, each sampled point matched exactly
by the surrogate. If we click over to the Error tab, you may see a little scatter, but this
is only from the (Nodeworks default) 10% holdout for cross validation. If we return to the
Model tab and set the cross validation points to 0 and refit the model, the parity
plot now shows a perfect 1:1 correlation and the error plot is near single precision numerical
zero.
However, it is unlikely that this, essentially error-free, surrogate is the best candidate.
Although analysis will not be covered in this example, typically the surrogate will be evaluated
at locations in the domain other than the exact sample locations. So, how much error does
the surrogate model incur in those instances? One way to answer this is through cross validation.
A random sub-set of the data are withheld and the surrogate is fit to the remaining data,
the error of which is evaluated with the hold out data. To assess the current surrogate model,
holdout 25% of the dataset for cross validation and re-fit the model. Repeat this procedure
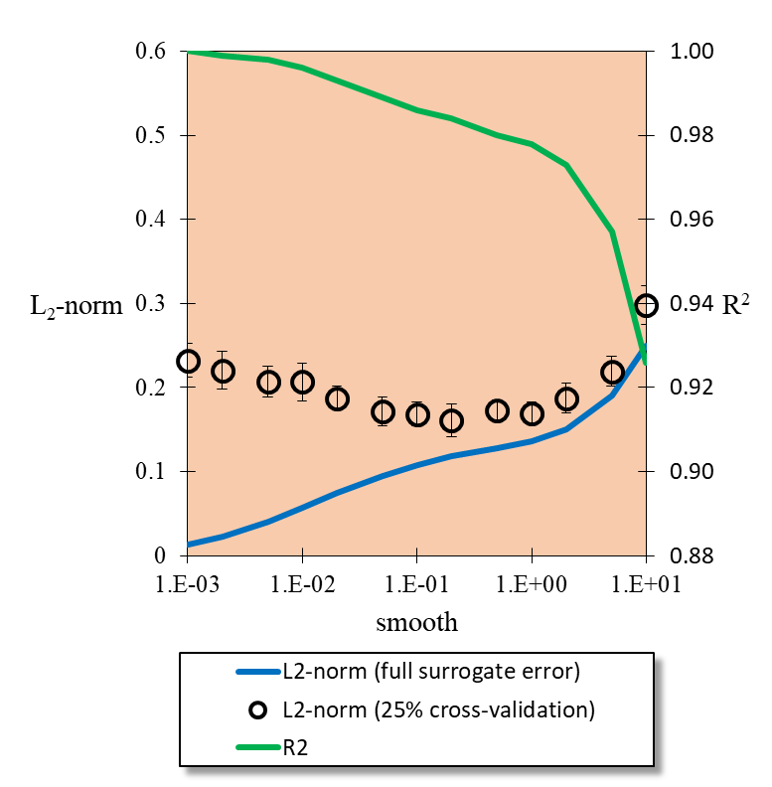
by incrementing the Smooth value and you should notice that the \(L_{2}-norm\) of the
error decreases at first before increasing. The image above shows the trends in full surrogate
\(R^2\) and \(L_2\) error, i.e., without cross validation holdout, and the error from
25% cross validation holdout with 95% confidence intervals from 10 replicate cross validation
fits. When the RBF acts as an interpolator, i.e., without smoothness, all of the noise
from the full model evaluation gets wrapped into the surrogate. (In this case we added our
Gaussian noise in intentionally, but in a real simulation this might be due to computational
errors such as convergence tolerances, statistical errors, etc.) As the smoothness is increased
we stop capturing the noise of each sample until we begin to smooth out some of the underlying
function. This is captured in the cross validation as a minimum in the holdout error.
Of course wider or tighter stencils, epsilon, or a different radial basis Function
or a different surrogate modeling choice altogether may produce an even better fit than
the model presented here. Users can test any of the different model options and compare
against the surrogate constructed here using the cross validation metrics.