Rotating drum(the dynamic angle of repose)

Zhangxutong · November 9, 2021, 2:14pm

Hello,everyone.
I would like to ask if the dynamic Angle of repose can be output at the moment of rotation of the drum. Need to add code?

cgw · November 9, 2021, 9:39pm

Hi Xutong. This is another case where you’re going to have to use some UDF (user-defined functions) to compute the quantity you are interested in. If you come up with a good implementation for AoR, you can share it here.

Searching the MFiX forum, there have been a few mentions of Angle of Repose in the past, but there’s no working examples.

Good luck!

– Charles

cgw · November 9, 2021, 9:44pm

On further reflection, you might be able to use a monitor for this: perhaps monitoring the mean particle location (i.e. center of mass of particles) would suffice.

Just look at how far from the vertical the center of mass is. A simple arctan of the (center-of-particle-mass - center-of-cylinder) should get you the AoR

–Charles

cgw · November 9, 2021, 10:30pm

Unfortunately, there is no monitor for particle position. you’re going to have to write a UDF.

Zhangxutong · November 10, 2021, 6:42am

Do you know which.f file to write udF in? Thank you!@cgw

cgw · November 16, 2021, 7:58pm

I made a very simple implementation of this idea in the rotating_drum tutorial. Here’s the changes I made to usr1_des.f:

--- /home/cgw/Work/NETL/mfix/tutorials/dem/rotating_drum_3d/usr1_des.f	2021-07-28 07:45:00.972978590 -0500
+++ ./usr1_des.f	2021-11-16 13:42:54.119068198 -0600
@@ -35,11 +35,17 @@
         use discretelement
         use run
         use usr
-  
+        use constant, only: pi
+
         implicit none
-        
+
+        double precision :: mean(3)
         integer :: i
 
+        mean = sum(des_pos_new, 1) / max_pip
+        write(*,*) "MEAN POS", mean
+        write(*,*) "ANGLE", 180*atan2(mean(2), mean(1))/PI + 90
+
 ! Interpolate data only in root process
         if(mype == pe_io) then
           call interpolate_keyframe_data(time)

The variables max_pip and des_pos_new are defined in the module discreteelement, for which we already have a use statement, so they are already accessible.

All this does is compute the center of mass of all the particles, and then how far from the vertical axis that is. When the particles are settled, this should match the angle of repose. But note that this computation will always return some angle, even when the angle of repose is not well-defined (like at the beginning of the simulation before all the particles have dropped). It’s up to you to decide if this algorithm is good enough or if you need some fancier way to compute angle of repose. This code is just to test the idea - it doesn’t handle DMP, for example, and the data needs to be saved in a better format (this just writes to the console). Here’s a plot of the reported angle during the run of rotating_drum (the drum reverses direction part way through)

angle

Please let me know if this is useful,

– Charles

cgw · November 16, 2021, 9:09pm

Here’s another run, with the direction reversal removed. The drum rotates at a constant rate for the first 8 seconds of the simulation, then is stopped.

You can see that the computed AoR oscillates for a bit at the beginnng, then takes quite a while to settle down. This could be because the algorithm is sensitive to statistical outliers, or perhaps it’s a real effect - it may take a few seconds for the balls to find their optimum packing and to lose their kinetic energy from the initial drop.

You’ll have to decide if this center-of-mass-based approach is good enough, or if you have to do some more complex measurements to determine AoR.

plot

cgw · November 17, 2021, 12:09am

@Zhangxutong -
here’s a much better result. In the above plot I did not understand that the values in data_kf_0001.txt were being interpolated in a linear ramp - so the background slope in the plot above is due to the drum slowing down, which I didn’t intend.

Here’s another run, with the data_kf_0001.txt set up as follows:

5, 1
linear
! time var1
0.0   0
0.5   0
1.0   20.0
6.0  20.0
6.5  0

This keeps the drum from rotating for the first 0.5 s, while the particles settle. Having the drum stationary while the particles fall reduces the size of the initial oscillation. The AoR is just below 0.

Then from 0.5s to 1s the drum accelerates, then keeps steady for 5s. In the plot the region from 1 to 5s shows a fairly stable dynamic angle of repose, after the initial oscillations die out. The value is around 35.5 degrees as can be seen in the “Detail” plot.

From 6s to 6.5s in the plot the drum is decelerating, then stops, where the AoR reaches its final steady value of 19.5.

Another change from the previous run is that I fixed an error in the code, it is possible that the des_pos_new array is larger than the number of particles, so my computation of the mean position was subject to extra junk at the end of the array. I changed my usr1_des.f to this:

        mean = sum(des_pos_new(1:particles,:), 1) / particles
        write(*,*) "ANGLE", 180*atan2(mean(2), mean(1))/PI + 90

cgw · November 17, 2021, 12:10am

plot1

plot3

jeff.dietiker · November 17, 2021, 1:00pm

Very nice Charles!

The second line of the keyframe file sets the interpolation type between data points. Available options are linear for linear interpolation and step for no interpolation. The Conveyor_belts.pdf file in the conveyor dem tutorial has more details.

cgw · November 17, 2021, 8:32pm

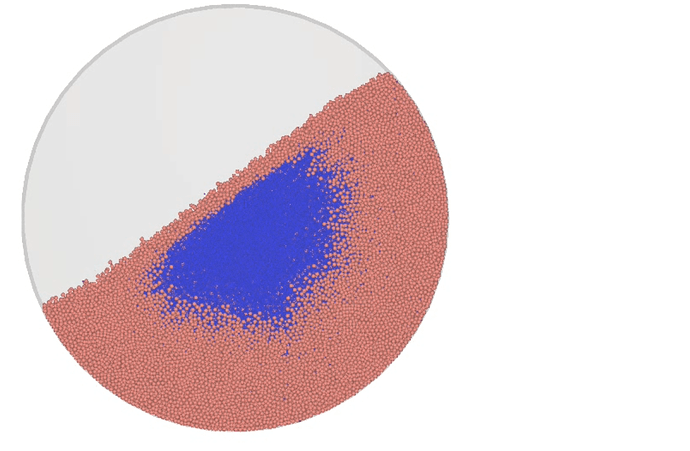
This animation shows the computed (statistical) angle of repose as a series of parallel lines drawn across the image. Note that an angle is always computed, even when the particles are not in a settled state, hence the strange result in the first few frames.

When the particles are settled, the fit looks quite good.

When the top surface is not flat, it’s a little harder to decide.

It will be up to you to determine whether this approach is adequate for your purposes.

Zhangxutong · November 20, 2021, 1:22pm

Thanks for your help. I’ll try it right now！@cgw

Zhangxutong · November 20, 2021, 2:48pm

Hello,@cgw
Thank you for your method. I just ran it successfully!

julia.hartig · November 29, 2021, 7:08pm

Charles,

How did you create the frames for this animation? The lines superimposed on the drum are a really nice visual aid!

cgw · November 29, 2021, 9:14pm

Thanks Julia.

It was a bit ad-hoc, I saved the output as an “image stack”, then used a little Python script to draw the lines using the ImageMagick utility. Note that there is a library for calling ImageMagick from Python but I didn’t use it, my script just computed the line endpoint coordinates and issued commands like:

convert -draw "line 0,0 1086,858" -draw "line 1086,0 0,858" -draw "line 543,0 543,858" x.png y.png

using os.system calls (primitive but effective). Then, after creating all the annotated frames, I put them together using ffmpeg, with a command like:

ffmpeg -r 30 -f image2 -i foo%03d.png -vcodec libx264 -pix_fmt yuv420p z.mp4

I’m sure there are many better ways to do this, but this was my ad-hoc approach using the utilities that were already installed and familiar to me.

– Charles

julia.hartig · November 29, 2021, 11:56pm

Charles,

I see, so I assume some component of your Python script takes the drum’s geometry as an input (diameter/circular intersection with your lines) to calculate the line endpoint coordinates?

I haven’t heard of the ImageMagick utility before so thank you for bringing it up!

cgw · November 30, 2021, 12:01am

Exactly. In this case it was pretty simple because the center of the drum is right in the center of the image, and I measured the radius empirically (in pixels). I’d share the script I used but I’m afraid I didn’t save it after I was done!

julia.hartig · November 30, 2021, 12:04am

Charles,

No worries, I was mostly interested in your thought process/workflow overall, which makes sense now!