Granular Rayleigh-Taylor

The Rayleigh-Taylor (RT) instability, along with the Kelvin-Helmholtz instability, is among the most well-known and fundamental of all multi-phase flow instabilities [C81]. The prototypical case involves two (traditional) fluids at rest of differing densities with the heavier fluid being accelerated into the lighter fluid. The instability manifests itself in a deformation of the interface between the two fluids. The initial deformation grows into an interpenetrating fingering pattern, commonly producing a mushroom cloud pattern, before giving way to micro-scale mixing or bubble-droplet formation if the fluids are immiscible.

Vinningland and coworkers [VJFTM07] devised a granular analogue of the classic problem in which the heavier “fluid” is an assembly of particles penetrating into a gas, in this case air. The particle assembly is generated by settling under gravity into a random close packed array in a Hele-Shaw cell (rectangular enclosure) which is quickly inverted around a pivot to bring the heavier particle phase above the lighter gas phase. The instability evolution is distinct from the classic fluid-fluid RT, which is described by Vinningland et al. [VJFTM07]:

The initially flat front defined by the grains subsequently develops

into a pattern of falling granular fingers separated by rising bubbles

of air. A transient coarsening of the front is observed right from the

start by a finger merging process. The coarsening is later stabilized

by new fingers growing from the center of the rising bubbles.

The granular-RT is simulated with MFIX-Exa 19.08 with the following setup. The domain is 56 mm wide by 68 mm tall and 1 mm deep which is discretized by a uniform mesh of \(224 \times 272 \times 4\) CFD cells. No-slip walls are applied at top, bottom, left and right domain extents. The front and back walls are “removed” and treated as periodic in the simulation as the depth is only resolved by four CFD cells. No additional geometry definition is required. The particles are assumed monodisperse with a constant diameter of \(d_p = 140\) microns (\(dx^* \approx 1.8\)) and density of \(\rho_p = 1050\) kg/m³ . The resitution and sliding friction coefficients are set to 0.9 and 0.25, which are believed to be representative of the polystyrene material. The WenYu drag law of Wen and Yu drag [WY66] is applied. 1.12M particles are initially randomly distributed throughout the domain. The gravity force on the particles is modified by \(\tanh 100(t - 2)\) so that the particles initially settle upwards, and then the body force is quickly inverted around \(t = 2\) s, causing the particles to fall downward into the quiescent air.

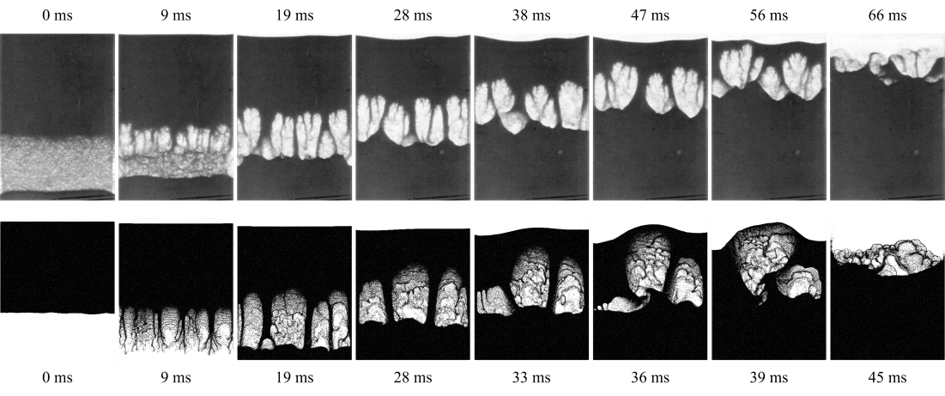
Fig. 22 Progression of the granular Rayleigh-Taylor instability in the experiments of Vinningland et al. [VJFTM07] (top row) compared to the MFIX-Exa result (bottom row).

The figure above shows the progression of an MFIX-Exa 19.08 simulation compared to the experimental results. There is a good match between the experimental and numerical results for roughly the first half of the transien: an initially flat interface gives way to many fingers falling into the gas which merge and form a semi-stable bubble pattern. However, the simulated bubbles appear to be less stable than those in the lab, which rise uniformily to the surface. However, in the simulations the center bubble rises slightly faster than the one on the left, which shifts more weight over the left-hand bubble, which further impedes its rise and eventually “squishes” the left-hand bubble into the center bubble as it breaks the surface. Later, the right hand bubble also merges with (what remains of) the center bubble, allowing a path of least resistance for its air to escape without rupturing on the surface on its own. The bubble merging significantly accelerates the second half of the transient (notice the different times between experiment and simulation). Several different variations of this setup were performed: different drag laws, slower inversion time, different combinations of particle restitution and friction coefficients, inclusion of front and back walls. Although all tests were slightly different, none were able to match the stability of the later time bubble pattern observed experimentally.