Ex. 2: Optimization

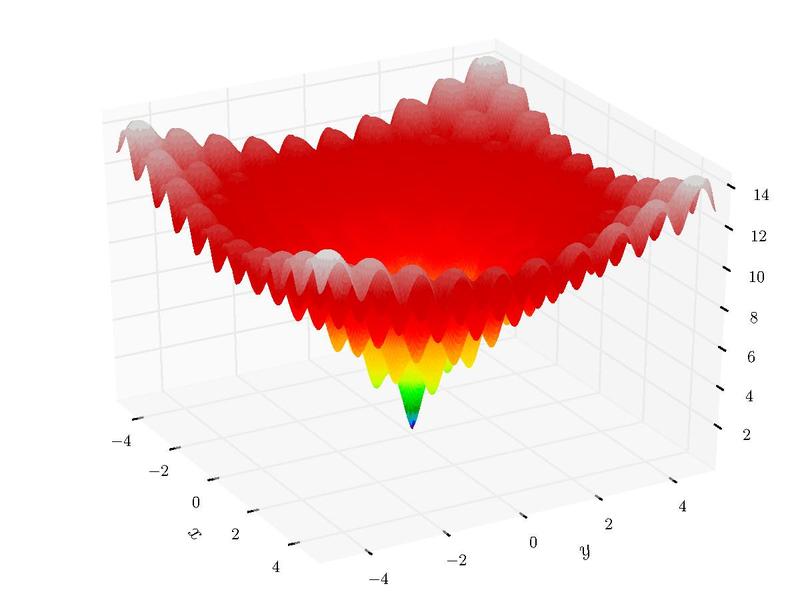
This example demonstrates the optimization of the Ackley function, which is commonly used to test the performance of optimization algorithms. The function has many local minima and one global minimum at \(f(0,0)=0\).

\[f(x,y)=-20exp[{-0.2\sqrt{0.5(x^2+y^2)}}] - exp[{0.5(cos 2 \pi x + cos 2 \pi y)}] + e + 20\]

Populate the Nodes

The Node Wizard conveniently provides functionality to populate all the nodes and provides a collection of optimization test functions, including the Ackley function. To construct the workflow quickly and focus on the optimization aspect, use the wizard by:

1. Click on the button to launch the wizard.

2. Click on the Optimization tab and set the Function to be optimized to Ackley and level the Method as surrogate.

3. Click Populate Nodes

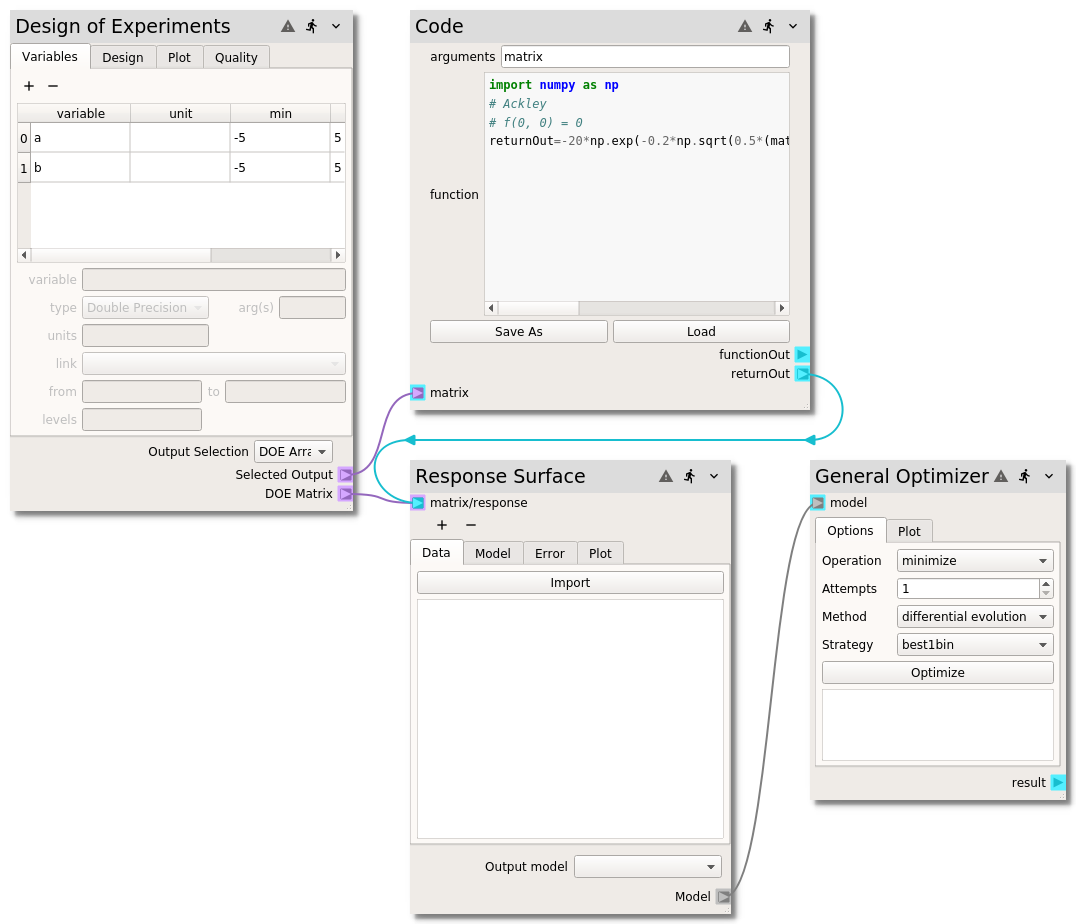
You should now have a collection of nodes including:

1. a Design of Experiments node with two variables, using the hammersly method with 1000 samples

2. a Code node with the Ackley function

3. a Response Surface node with the radial basis function selected, and

4. a General Optimizer node

that looks like this:

Local Optimization

To demonstrate the challenge with black-box optimization, we will first try using a local minimization method:

1. On the General Optimizer, change the number of attempts to 10.

2. Select local from the Method combo-box. The Local Method combo-box should appear with the Nelder-Mead method selected.

3. Run all the nodes by pressing button on the application toolbar.

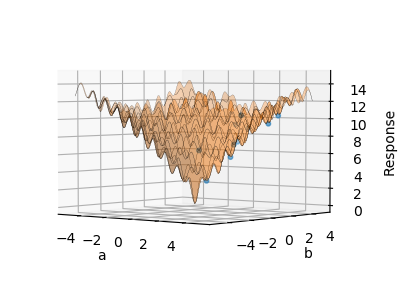
After all the nodes have been run, the results of the 10 minimization attempts are displayed. Notice how each of the 10 attempts seems to provide a different “optimum”. This happens because each attempt has an initial condition which is randomly picked from inside the ranges of the variables specified in the Design of Experiments node. This local minimization method frequently gets stuck in the many local minima of the Ackley function.

The attempts can be visualized on the Plot tab of the General Optimizer node, where the surface is the sampled function and the dots are the optimization attempts. Note how these particular attempts never found the global minimum:

Global Optimization

Global optimization routines try to avoid getting stuck in local minima. One method provided in the General Optimizer node that works well is Differential Evolution.

To use this method:

1. select differential evolution from the Method combo-box

2. press the Optimize button on the General Optimizer node

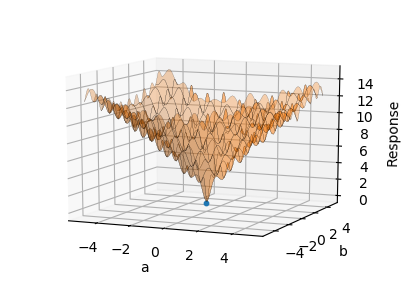
After the node has run, all 10 optimization attempts should be roughly the same value, \(f(-0.02, -0.02)=0.19\). The differential evolution algorithm did a good job of avoiding the local minimas and finding the true minimum. Unfortunately, this value is not precisely the true minimum, which should be \(f(0,0)=0\). The problem is that there are not enough samples at or around the true minimum for the surrogate model, constructed in the Response Surface, to accurately represent the sharp minimum of the Ackley function.

Response Surface Refinement

After an optimum has been found, the response surface can be refined around that optimum to get closer to the true optimum. In this particular case, lets see if we can get closer to the mathematical optimum. To do this, we will leave the original samples in-place and add new samples around the optimum:

1. Duplicate the Design of Experiments node and Code node by

   1. Selecting the Design of Experiments node by clicking on the title.

   2. While holding Ctrl on the keyboard, select the Code node by clicking on its title.

   3. Copy the selected nodes by either pressing Ctrl + c on the keyboard or right-click and select Copy from the menu.

   4. left-click to the left of the Response Surface node.

   5. Paste the nodes by pressing Ctrl + v on the keyboard or right-click and select Paste from the menu.

2. Add a Matrix/Response terminal to the Response Surface node by pressing the button below the existing Matrix/Response terminal.

3. Connect the terminals of the copied nodes by

   1. Connecting the Selected Output terminal of the copied Design of Experiments node to the matrix terminal of the copied Code node.

   2. Connecting the returnOut terminals of the copied Code node to the new Matrix/Response 1 terminal of the Response Surface node.

   3. Connecting the DOE Matrix terminal of the copied Design of Experiments node to the new Matrix/Response 1 terminal of the Response Surface node.

4. Adjust the variable ranges of the copied Design of Experiments node by

   1. Select the variable tab

   2. Select variable a and changed the from value to -0.1 and the to value to 0.1.

   3. Select variable b and changed the from value to -0.1 and the to value to 0.1.

   4. On the Design tab, change the number of Samples to 100.

   5. On the Design tab, press the Build button to build the samples.

5. Adjust the response surface in the Response Surface node node by

   1. Select the Model tab

   2. Select the radial basis function from the table.

   3. Change the Function from multiquadric to cubic

6. Run all the nodes by pressing button on the application toolbar.

By adding the additional samples, the found optimum (\(f(-0.0007, 0.001)=0.02\)) is closer to the analytic solution (\(f(0,0)=0\)). You should have a workflow that looks like this:

Note

See how close you can get to the true solution of \(f(0,0)=0\) by changing the samples and response surface model settings.