Ex. 5: Deterministic Calibration¶
Suppose we have a complex model with numerous unknown parameters that we want to calibrate to experimental data (well not that complex):
Where the model inputs are \(x\) and \(y\), and \(a\) and \(b\) are unknown model parameters. We can use nodes available in nodeworks to explore a collection of \(a\) and \(b\) parameter values and fit a surrogate model to the response. We can then evaluate the surrogate model at experimental conditions and compare the response of the surrogate model to the experimental response. Finally, we can calibrate the \(a\) and \(b\) parameters to the experimental data using the optimization node.
Step 1: Sample the model¶
We need to generate samples for all four variables. To do this, add a Design of Experiments node. Add the four variables and adjust the ranges to match the following:
Variable |
From |
To |
x |
-1.0 |
1.0 |
y |
-1.0 |
1.0 |
a |
1.0 |
4.0 |
b |
1.0 |
4.0 |
Next, go to the Design tab of the Design of Experiments node. Change the Method
to latin hypercube and the samples to 100. Finally, press Build
to generate the samples.
Add a Code node next to the Design of Experiments node. Create a new terminal by
entering “samples” in the arguments field. Copy and paste the following
python code into the editor. This code will evaluate the model for each sample.
import numpy as np
s = np.abs(np.asarray(samples[1:]))
returnOut = s[:,0]**s[:,2] + s[:,1]**s[:,3]
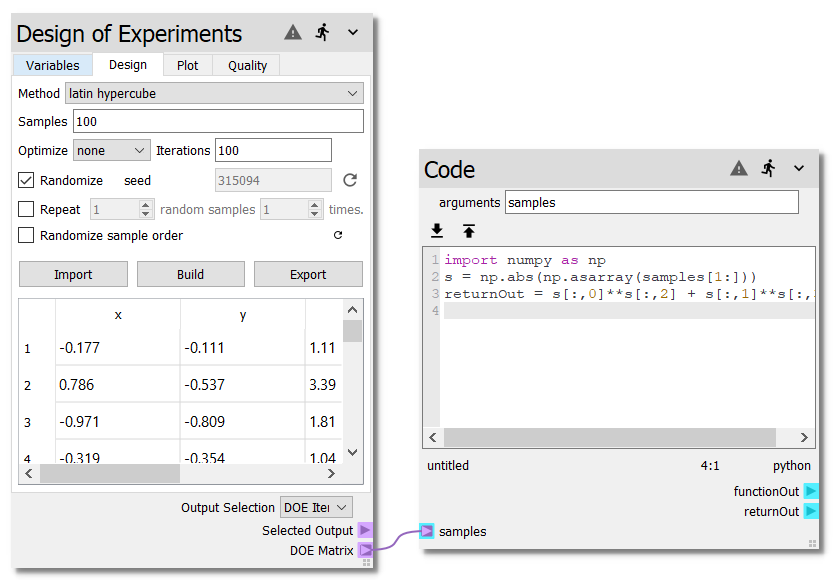
Finally, connect the DOE Matrix terminal of the Design of Experiments node to the
samples terminal of the Code node. Your sheet should now look like the
following:
Step 2: Build the surrogate¶
Now we will construct a surrogate model to represent the response of the model.
Add a Response Surface node next to the Code node. Connect the returnOut
terminal from the Code node to the matrix/response terminal on the
Response Surface node. Next, connect the DOE Matrix terminal of the
Design of Experiments node to the matrix/response terminal on the Response Surface
node.
On the Model tab of the Response Surface node, check the check mark next to
the radial basis function model. Run the sheet by pressing the
button. The sheet should now look like:

Step 3: Generate experimental data¶
For this particular example, we are going to generate experimental data. This
allows use to play with the experimental data and explore the effects of samples
and noise on the effectiveness of the calibration. You can also read data from
*.csv files.
Add another Code node below the Response Surface node. Copy and paste the
following python code into the editor.
import numpy as np
n = 100 # samples
a = 2 # model parameter
b = 3 # model parameter
sigma = 0.01 # std of the noise
# generate random x, y samples
s = np.random.uniform(-1, 1, size=(n, 2))
# make some noise!
noise = np.random.normal(0, sigma, n)
# calculate the response
r = np.abs(s[:,0])**a + np.abs(s[:,1])**b + noise
# combine the samples (x, y) with the response (r)
returnOut = np.hstack((s, np.atleast_2d(r).T))
Step 4: Calibrate¶
We are now ready to compare the model with the experimental data and minimize
the error. Add a Residual Function node next to the Response Surface node.
Connect the Model terminal of the Response Surface node to the model
terminal of the Residual Function node. Also, connect the returnOut from
the second Code node to the experimental data terminal of the
Residual Function node.
Press to run the sheet and populate the table of the Residual Function
node. Now that the table is populated, we can map the experimental values to the
model inputs. You will see the red error indication around Residual Function
node with Show Error message icon on the top right of the node, which is normal
as the Experimental dataset is not mapped to the surrogate model parameters.
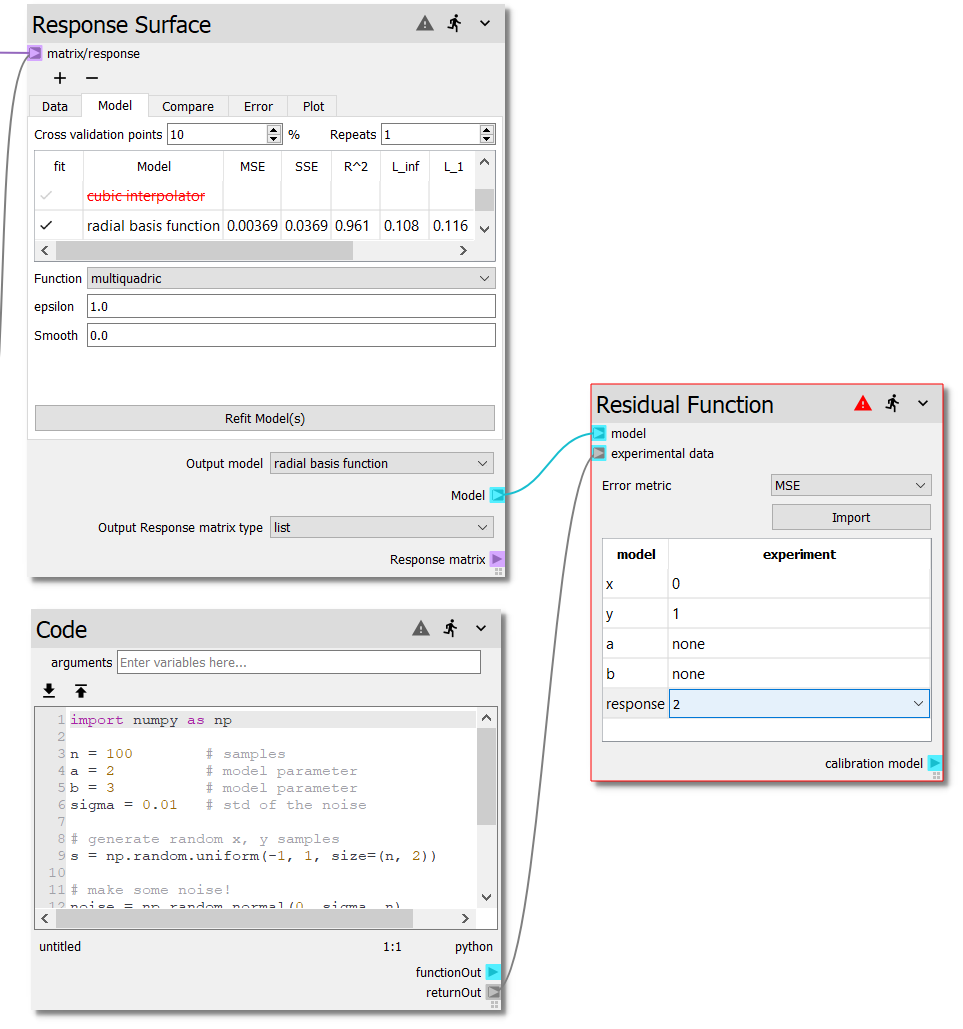
To map the experimental values to the model parameters, Double-click the
cell on the x row, experiment column and select 0 from the
combo-box. This will map the first column of the experimental data to the
\(x\) value of the model. Likewise, select 1 for the y row and 2
for the response row. Your sheet should now look like the following.
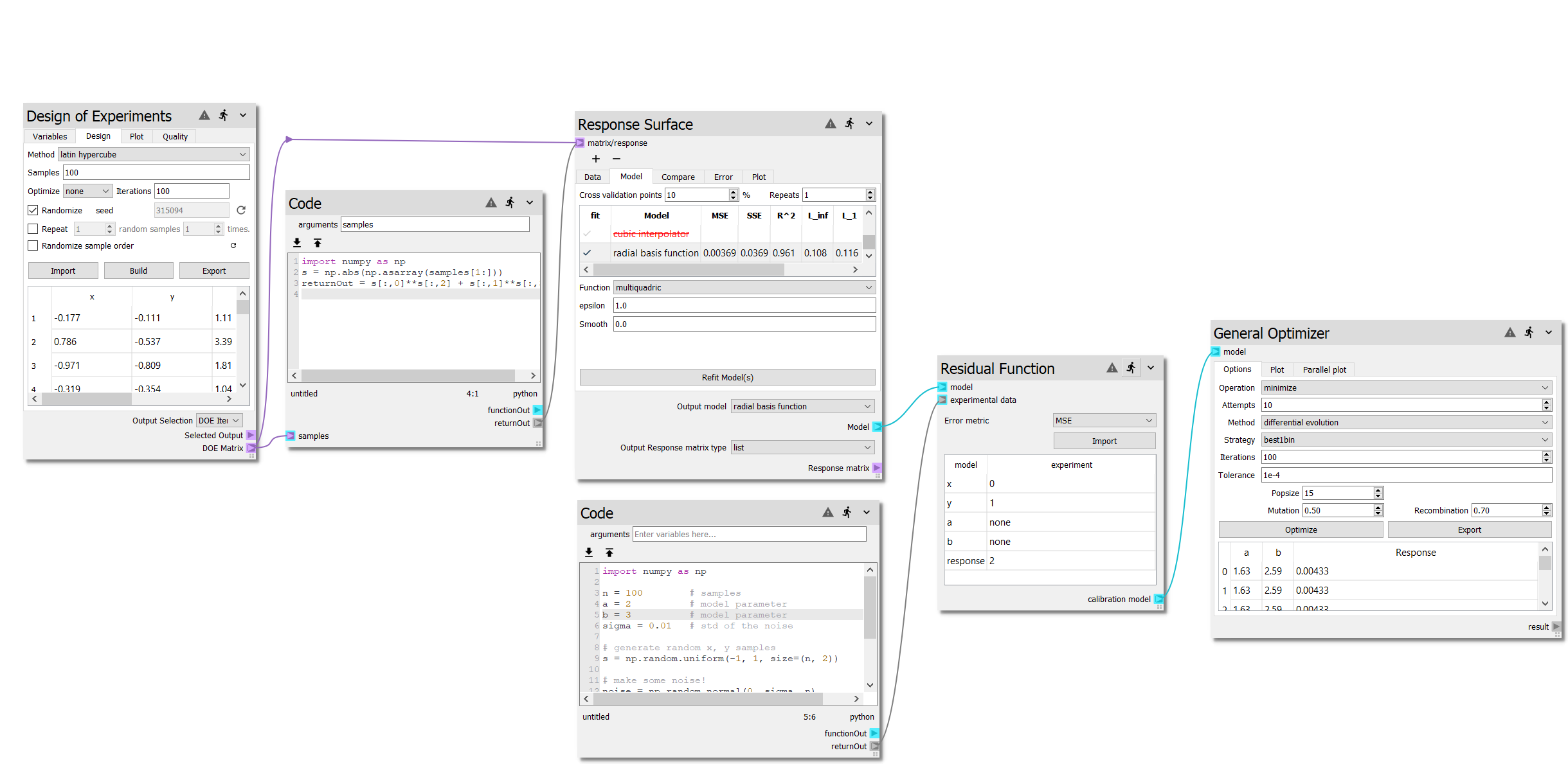
Finally, add a General Optimizer node next to the Residual Function node.
Connect the calibration model terminal of the Residual Function node to
model terminal of the General Optimizer node. On the General Optimizer
node, change the number of attempts to 10. Finally, press to run the
sheet. The complete sheet should look like the following, note that the Latin
Hypercube samples in Response Surface node and optimization results shown in
General Optimizer might be different form your worksheet due to random sample
generation:
Step 5: How close did it get?¶
In the second code node, we specified \(a = 2\) and \(b = 3\) when generating the experimental data. The General Optimizer node minimized the error between the model and the experiment data. In this particular instance, out of the 10 optimization attempts, the minimum error resulted in \(a = 1.63\) and \(b = 2.59\). So why are these not exactly \(a = 2\) and \(b = 3\)?
Well, there are random processes involved in generating the samples and noise
added to the experimental data. Play with the number of model samples
(Design of Experiments node), using other surogate models (Response Surface node),
and the amount of samples and noise in the experimental data (n and
sigma in the second Code node). How close can you get?
For example, changing the number of samples of the model from 100 to 500
in the Design of Experiments node and re-running the sheet resulted in a more accurate
response surface. The General Optimizer then found the optimal values to be
\(a = 1.97\) and \(b = 3.18\).