4.1. DEM01: Freely-falling particle

This case serves to verify the MFIX-DEM linear spring-dashpot collision model as well as the accuracy of the time-stepping methods. This case is based on the work of Chen et al. [4] and the MFIX-DEM case was originally reported in Garg et al. [8].

4.1.1. Description

A smooth (frictionless), spherical particle falls freely under gravity from an initial height, \(h_{0}\), and bounces upon collision with a fixed wall. The translating motion of the particle is described in three stages, as depicted in Fig. 4.1. An analytic expression for particle motion during each stage is obtained.

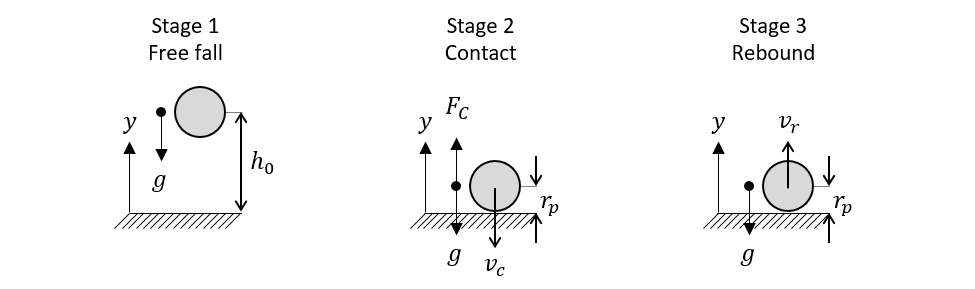
Fig. 4.1 A particle with radius \(\mathbf{r}_{\mathbf{p}}\) falling onto a fixed wall from an initial height of \(\mathbf{h}_{\mathbf{0}}\) where \(\mathbf{g}\) is the gravitational force, \(\mathbf{F}_{\mathbf{C}}\) is repulsive particle-wall collision force, \(\mathbf{v}_{\mathbf{c}}\) is the pre-collision particle velocity, and \(\mathbf{v}_{\mathbf{r}}\) is the post-collision particle velocity.

Stage 1: Free fall

A force balance on the particle provides an expression for particle motion during free fall,

(4.1)\[\frac{d^{2}y}{dt^{2}} = - g;\quad y\left( 0 \right) = h_{0};\quad \frac{\text{dy}}{\text{dt}}(0) = 0\]

where \(y\) is the center position of the particle with respect to the wall and \(g\) is the acceleration due to gravity. The particle is initially at rest with a center distance of \(h_{0}\) above the wall. The instantaneous velocity, \(v\), and particle center position are given by

(4.2)\[v\left( t \right) = - gt\]

(4.3)\[y\left( t \right) = h_{0} - \frac{1}{2}gt^{2}\]

Stage 2: Contact

The free fall stage ends and the contact stage begins when the particle center position is equal to the particle radius. The particle-wall collision is treated using the linear spring-dashpot model such that the force balance on the particle during contact gives

(4.4)\[\begin{split}&\frac{d^{2}y}{dt^{2}} + 2\beta\omega_{o}\frac{\text{dy}}{\text{dt}} + \omega_{o}^{2}y = \omega_{o}^{2}r_{p} - g;\\ &y\left( 0 \right) = r_{p};\quad \frac{\text{dy}}{\text{dt}}\left( 0 \right) = - \sqrt{2g\left( h_{0} - r_{p} \right)}\end{split}\]

where \(\beta = \eta_{n}/\left( 2\sqrt{k_{n}m_{p}} \right)\) and \(\omega_{o} = \sqrt{k_{n}/m_{p}}\). Here, \(k_{n}\) and \(\eta_{n}\) are the normal spring coefficient and damping coefficients for the particle-wall collision, and \(m_{p}\) is the particle mass. The initial particle velocity is obtained from combining Eq.4.2 and Eq.4.3 when the particle center position is equal to its radius. The instantaneous velocity and particle center position during contact for an underdamped system, \(\beta < 1\), are given by

(4.5)\[v\left( t \right) = \left\lbrack - \sqrt{2g\left( h_{0} - r_{p} \right)}\cos\left( \phi t\right) + \frac{\beta\omega_{o}\sqrt{2g\left( h_{0} - r_{p} \right)} - g}{\phi}\sin\left( \phi t \right) \right\rbrack\exp\left( - \beta\omega_{o}t \right)\]

(4.6)\[y\left( t \right) = \left\lbrack \frac{g}{\omega_{o}^{2}}\cos\left( \phi t \right) + \frac{- \sqrt{2g\left( h_{0} - r_{p} \right)} - \frac{\text{βg}}{\omega_{o}}}{\phi}\sin\left( \phi t \right) \right\rbrack\exp\left( - \beta\omega_{o}t \right) + \left( r_{p} - \frac{g}{\omega_{o}^{2}} \right)\]

where, \(\phi = \sqrt{1 - \beta^{2}}\omega_{o}\)

Stage 3: Rebound

The contact stage ends and the rebound stage begins when the particle center position is again equal to the particle radius. A force balance on the particle leads to an expression for the particle motion,

(4.7)\[\frac{d^{2}y}{dt^{2}} = - g;\quad y\left( 0 \right) = r_{p};\quad \frac{\text{dy}}{\text{dt}}\left( 0 \right) = v_{c}.\]

The velocity at the start of the rebound stage is equal to the velocity at the end of the contact stage, \(v_{c}\). It is obtained by solving Eq.4.6 for time when the particle center position is equal to the particle radius, then substituting the result into equation Eq.4.5. The instantaneous velocity, \(v\), and particle center position, \(y\), are given by

(4.8)\[v\left( t \right) = v_{c} - gt\]

(4.9)\[y\left( t \right) = r_{p} + v_{c}t - \ \frac{1}{2}gt^{2}.\]

4.1.2. Setup

Table 4.2 DEM-01 Setup, Initial and Boundary Conditions.

Computational/Physical model
1D, Transient
Granular flow (no gas)
Gravity
Thermal energy equation is not solved
Geometry
Coordinate system	Cartesian
x-length	1.0	(m)
y-length	1.0	(m)
z-length	1.0	(m)
Solids Properties
Normal spring coefficient, \(k_{n}\)	varied	(N·m-1)
Restitution coefficient, \(e_{n}\)	varied	( )
Friction coefficient, \(\mu\)	0.0	( )
Solids 1 Type	DEM
Diameter, \(d_{p}\)	0.2	(m)
Density, \(\rho_{s}\)	2600	(kg·m-3)
Boundary Conditions
All boundaries	Solid walls

4.1.3. Results

Simulations of a freely-falling particle dropped from an initial height of 0.5m were conducted for four particle-wall normal spring coefficients, \(\lbrack 1.0,\ 2.5,\ 5.0,\ 10.0\rbrack \times 10^{4}\) N·m^-1, and five restitution coefficients, [0.6, 0.7, 0.8, 0.9, 1.0]. The test using a normal spring coefficient of 10⁴ N·m^-1 and restitution coefficient 0.6 were unsuccessful because this combination leads to the particle center crossing the fixed boundary indicating that the particle is located outside of the domain. The following results were obtained using the Euler time stepping method.

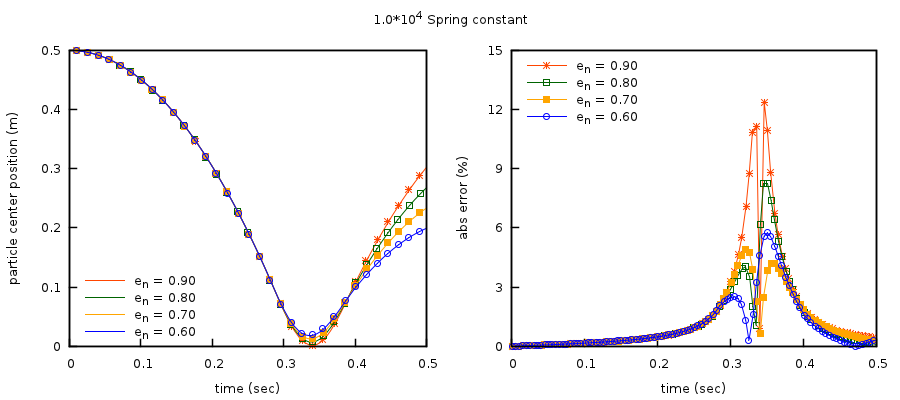
Fig. 4.2 Comparison of analytical solution and DEM results for a freely-falling particle using the Euler time-stepping method for varying restitution coefficient, normal spring coefficient, \(\mathbf{k}_{\mathbf{n}}\mathbf{= 1}\mathbf{0}^{\mathbf{4}}\) N•m^-1. (Left) Particle center position; analytical solutions shown as continuous lines, MFIX-DEM results as points. (Right) Percent absolute relative error between the analytical and MFIX-DEM particle center positions.

The particle center position for cases using a normal spring coefficient of 10⁴ N·m^-1 are shown in Fig. 4.2. These cases demonstrate the largest errors in particle center position during the contact stage. The large error is attributed to the particle center position approaching the fixed boundary, \(y \rightarrow 0\), during the contact stage. This leads to near-zero values used in the absolute value of the relative error calculations. In all other cases, the absolute percent relative error remains below 3% with errors decreasing with increasing normal spring coefficient.

The particle velocity for cases using a slightly stiffer normal spring coefficient of 10⁵ N·m^-1 are shown in Fig. 4.3. Again, the large errors are primarily attributed to near-zero values used in the relative error calculations. The initial spike in error arises at the peak of the contact stage when the particle trajectory reverses, passing through zero. Similarly, large relative errors occur at the peak of the rebound stage when the particle trajectory again reverses direction.

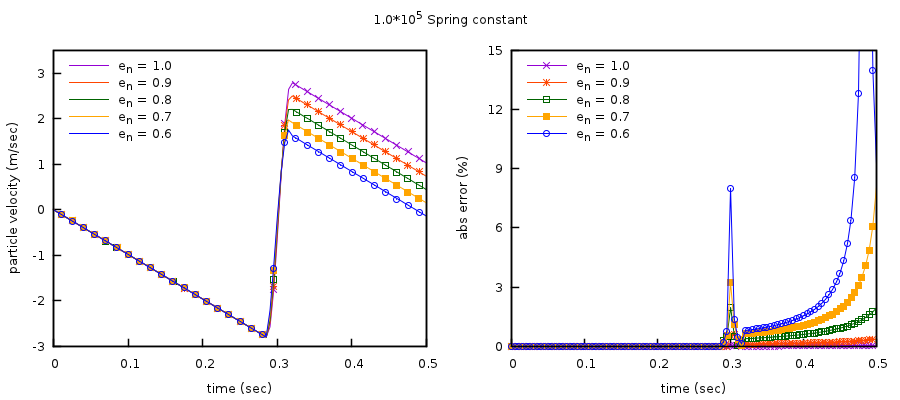
Fig. 4.3 Comparison of analytical solution and DEM results for a freely-falling particle using the Euler time-stepping method for varying restitution coefficients, and normal spring coefficient, \(\mathbf{k}_{\mathbf{n}}\mathbf{= 1}\mathbf{0}^{\mathbf{5}}\) N•m^-1. (Left) Particle velocities; analytical solutions shown as continuous lines, MFIX-DEM results as points. (Right) Percent absolute relative error between the analytical and MFIX-DEM particle velocities.

Analysis of the time-stepping methods is limited to the free-fall stage and excludes error arising from the collision model. Pre- and post-collision results using the Euler and Adams-Bashforth methods with a normal spring coefficient of 10⁵ N·m^-1 are shown in Fig. 4.4. During the free fall stage (pre-collision), the Euler method shows a linear accumulation of error in particle position whereas the error in particle velocity is zero. The Adams-Bashforth method shows no (zero) error for both particle position and velocity. These results are consistent across all cases.

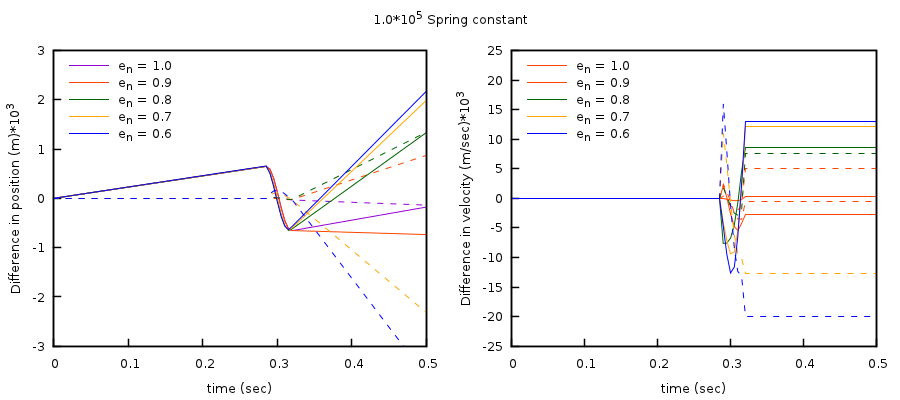
Fig. 4.4 Difference between analytical solution and MFIX-DEM results for a freely-falling particle with varying restitution coefficient and normal spring coefficient, \(\mathbf{k}_{\mathbf{n}}\mathbf{= 1}\mathbf{0}^{\mathbf{5}}\) N•m^-1. Euler method shown as solid line. Adams-Bashforth method shown as dashed lines. (Left) Difference in particle position. (Right) Difference in particle velocity.