4.4. DEM04: Slipping on a rough surface¶
This case serves to verify the MFIX-DEM soft-spring collision model through the analysis of the rolling friction model. This test case was originally reported in [8].
4.4.1. Description¶
A spherical particle of radius, \(r_{p}\), finite translation velocity, \(u_{0}\), and zero angular velocity, \(\omega_{0}\), is placed on a rough surface as illustrated in Fig. 4.9. The particle begins to roll while the translational velocity decreases because of rolling friction attributed to slip between the particle and the rough surface at the point of contact (\(u \neq \omega r_{p}\)). The rolling friction converts translation velocity to angular velocity until there is no slip at the contact point (\(u = \omega r_{p}\)). After the no-slip condition is reached, rolling friction ceases and the particle continues to move with constant translational and rotational velocities.

Fig. 4.9 A spherical particle with finite translational velocity and zero angular velocity is placed on a rough surface. Forces acting on the particle are indicated.¶
Kinetic friction is the only translational force acting on the particle and is given by
where \(g\) is the acceleration due to gravity, and \(\mu\) is the coefficient of friction. Similarly, the angular velocity is given by
where \(I = 2mr_{p}^{2}/5\) and \(m\) are the particle moment of inertia and mass, respectively. Integrating equations (4‑14) and (4‑15) with initial conditions \(u_{0}\) and \(\omega_{0}\), an expression for the time when rolling friction ceases (\(u = \omega r_{p}\)) is obtained,
4.4.2. Setup¶
Computational/Physical model |
|||
|---|---|---|---|
1D, Transient |
|||
Granular flow (no gas) |
|||
Gravity |
|||
Thermal energy equation is not solved |
|||
Geometry |
|||
Coordinate system |
Cartesian |
||
x-length |
1.0 |
(m) |
|
y-length |
1.0 |
(m) |
|
z-length |
1.0 |
(m) |
|
Solids Properties |
|||
Normal spring coefficient, \(k_{n}\) |
104 |
(N·m-1) |
|
Restitution coefficient, \(e_{n}\) |
1.0 |
( ) |
|
Friction coefficient, \(\mu\) |
varied |
( ) |
|
Solids 1 Type |
DEM |
||
Diameter, \(d_{p}\) |
0.001 |
(m) |
|
Density, \(\rho_{s}\) |
10,000 |
(kg·m-3) |
|
Boundary Conditions |
|||
All boundaries |
Solid walls |
4.4.3. Results¶
Simulations were conducted for nine restitution coefficients, [0.2, 0.3, 0.4, 0.4, 0.6, 0.7, 0.8, 0.9 1.0], using the Adams-Bashforth time-stepping method with the results shown in Fig. 4.10. The absolute relative percent error between the MFIX-DEM and analytical value for the non-dimensionalized time when rolling friction ceases, \(t_{s}/\left( \text{μg}/u_{0} \right)\), is less than 1% for all reported conditions. Similarly, the absolute relative percent error between the MFIX-DEM and analytical value for the non-dimensionalized tangential and angular velocities is less than 0.1% for all reported conditions. Error between the MFIX-DEM and analytical values can be further reduced (not shown) by increasing the normal spring coefficient, \(k_{n}\), which decreases the DEM solids time-step size.
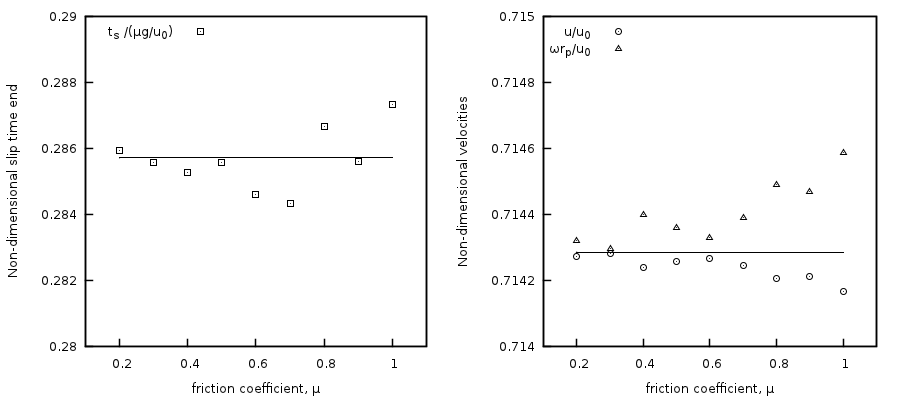
Fig. 4.10 Comparison between the analytical solution (solid line) and MFIX-DEM simulation (open symbols) of a particle with radius \(\mathbf{r}_{\mathbf{p}}\) slipping on a rough surface for various friction coefficients. (left) Dimensionless slip time end and (right) dimensionless equilibrium tangential, \(\mathbf{u}\), and angular, \(\mathbf{\omega}\), velocities.¶