4.6. DEM06: Single particle, terminal velocity

This case investigates the interphase coupling of momentum equations though the gas-solids drag force. The original case was reported in [8] and has been expanded to test additional coupling schemes.

4.6.1. Description

A single particle initially at rest is released in a uniform gas stream as illustrated in Fig. 4.14 where the gravitational and gas-solids drag forces are the dominant forces acting on the particle. The velocity of the particle increases until it reaches its terminal velocity where the gravitational force is equal to the gas-solids drag force.

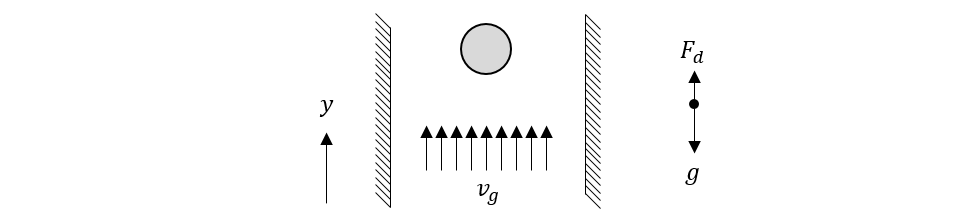
Fig. 4.14 A single spherical particle initially at rest is released in a uniform, vertical air flow. The dominant forces acting on the particle are the gas-solids drag force, \(\mathbf{F}_{\mathbf{d}}\), and the gravitational force, \(\mathbf{g}\).

For a sufficiently small particle, the evolution of the particle velocity is given by

(4.17)\[\begin{split}&\frac{d^{2}y}{dt^{2}} = \frac{dv_{p}}{\text{dt}} = \frac{g\left( \rho_{p} - \ \rho_{g} \right)}{\rho_{p}} - \frac{3}{4}\frac{\rho_{g}\left\| v_{p} - v_{g} \right\|_{2}}{d_{p}\rho_{p}}C_{d};\\ &y\left( 0 \right) = h_{0};\quad \frac{\text{dy}}{\text{dt}}(0) = 0\end{split}\]

where \(y\) is the particle center position measured from the bottom wall, \(v_{p}\) and \(v_{g}\) are the particle and gas velocities, \(\rho_{p}\) and \(\rho_{g}\) are the particle and gas densities, \(d_{p}\) is the particle diameter, \(h_{0}\) is the initial height of the particle, \(g\) is the acceleration due to gravity, and \(C_{d}\) is the drag coefficient. The drag coefficient is estimated here using the Schiller and Naumann [27] correlation for a single particle in an unbounded medium,

(4.18)\[C_{d} = \frac{24}{N_{\text{Re}}}\left( 1 + 0.15N_{\text{Re}}^{0.687} \right)\]

where \(N_{\text{Re}}\) is the Reynolds number based on the slip velocity between the particle and gas defined as

(4.19)\[N_{\text{Re}} = \frac{\rho_{g}\left\| v_{p} - v_{g} \right\|_{2}d_{p}}{\mu_{g}}.\]

4.6.2. Setup

Table 4.8 DEM-06 Setup, Initial and Boundary Conditions.

Computational/Physical model
1D, Transient
Multiphase flow (gas-solids)
Gravity
Thermal energy equation is not solved
Geometry
Coordinate system	Cartesian
x-length	0.01	(m)
y-length	0.10	(m)
z-length	0.01	(m)
Solids Properties
Normal spring coefficient, \(k_{n}\)	10-1	(N·m-1)
Restitution coefficient, \(e_{n}\)	1.0	( )
Friction coefficient, \(\mu\)	0.0	( )
Solids 1 Type	DEM
Diameter, \(d_{p}\)	10-4	(m)
Density, \(\rho_{s}\)	2,000	(kg·m-3)
Boundary Conditions
South face (XZ-plane; y=0.00m)	Gas Mass Inflow
Pressure (gauge)	0.00	(Pa)
Gas velocity, \(v_{g}\)	0.40	(m·s-1)
North face (XZ-plane; y=0.10m)	Pressure Outflow
Pressure (gauge)	0.00	(Pa)
All other boundaries	Free-slip walls

4.6.3. Results

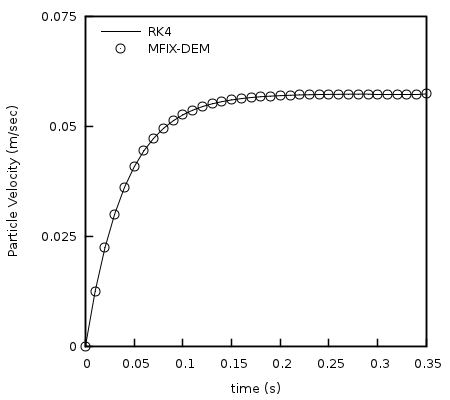
A fourth-order Runge-Kutta method was used to calculate the solution to Eq.4.17 which was subsequently compared with the solutions of the seven MFIX-DEM simulations outlined below. The first set of simulations were one-way coupled such that only the gas phase volume fraction was affected by the presence of the particle. Specifically, gas-solids drag force was omitted from the gas phase momentum equations. This case best captured the above problem description where a single particle is freely falling through a uniform gas field. In the second group of tests the gas and solids were fully coupled. Three interpolation methods were used with both the one-way and fully coupled tests.

Table 4.9 Gas-solid interpolation.

Interpolation Scheme	Coupling	Filter size
Centroid	one-way	–
Garg_2012	one-way	–
DPVM_Square	one-way	2.0 x 10-3
Centroid	full	–
Garg_2012	full	–
DPVM_Square	full	3.0 x 10-3
DPVM_Square	full	4.0 x 10-3

Fig. 4.15 illustrates a typical comparison of analytical particle velocity evolution over time obtained by Eq.4.17 and the numerical solution. A comparison of the absolute percent relative difference between the solutions is shown in Fig. 4.16. The numerical solution from simulations employing one-way coupling (left) compare well with the analytical solution of Eq.4.17 with the maximum absolute relative difference bounded above by \(5 \times 10^{- 3}\) percent for the three cases. Additionally, the maximum absolute relative difference for cases with full coupling is bounded from above by \(5\) percent.

Fig. 4.15 Comparison of the particle velocity evolution obtained by Eq.4.17 and MFIX-DEM.

The large difference in results for the fully coupled cases should not be interpreted as error because the assumption of a uniform gas velocity used to establish Eq.4.17 is no longer valid when the gas-solids drag is allowed to affect the gas velocity as is the case in the fully coupled simulations. The suitability of this assumption, or lack thereof, is apparent from inspecting the results from different coupling schemes. The centroid method concentrates the gas-solids drag force in the fluid cell containing the particle center. As a result, gas velocity is impacted the most when compared to the other methods available. The divided particle volume method (DVPM) diffuses the gas-solids drag force over an area based on the filter width providing better agreement. Finally, the GARG_2012 scheme shows the best agreement as it diffuses the gas-solids drag force over the greatest area thereby providing greater consistency with the uniform flow field assumption.

Fig. 4.16 Absolute percent relative difference between particle velocity evolution obtained by Eq.4.17 and MFIX-DEM. (left) Simulations with one-way gas-solids coupling. (right) Fully coupled simulations.