Home » Research » Software Development » MFiX Software Quality Assurance
MFiX Software Quality Assurance
Integrated Verification, Validation and Uncertainty Quantification (VVUQ) Framework
The complexity of governing physics in multiphase flows necessitates various assumptions to be incorporated in the MFiX model development. In addition, the input conditions to run the MFiX models may have some uncertainties. The objective of the verification, validation and uncertainty quantification (VV&UQ) framework is to assess the credibility of MFiX simulation results for various flow configurations of interest by considering these modeling assumptions and sources of various uncertainties. An integrated approach is employed by leveraging the well-established Verification and Validation (V&V) Standards (e.g., ASME V&V 20) and the Laboratory Studies at NETL for carrying out physical experiments to support the validation studies. In addition to other open-source UQ toolkits (e.g., PSUADE, DAKOTA), Nodeworks developed at NETL is heavily employed for constructing and executing the scientific workflows for various UQ analysis.
The activities under the VVUQ framework are mainly comprised of the following:
- Verification and Validation (V&V) Studies
- Uncertainty Quantification (UQ) Assessment Studies
- Calibration Studies
Verification, Validation and Uncertainty Quantification Workflow
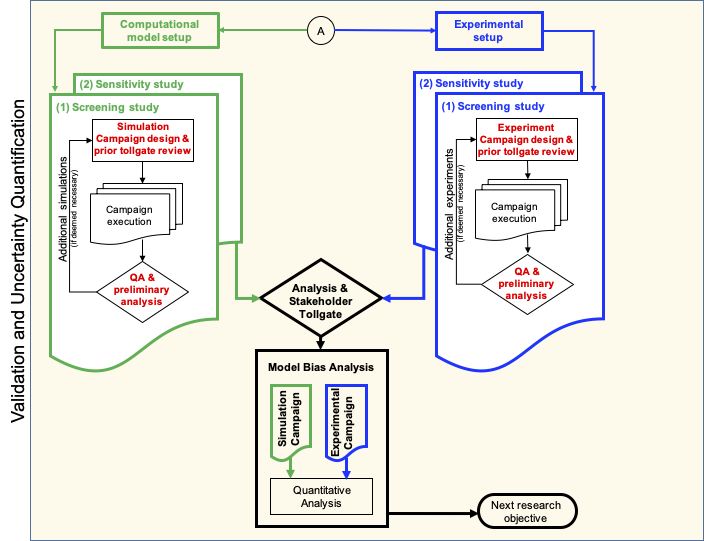
The Verification, Validation and Uncertainty Quantification workflow developed and employed for multiphase flows consists of multiple phases and toll gates to ensure consensus among all stakeholders within each phase. An overview of the workflow is illustrated in the figures on the right. Additional details can be found in Gel et al. (2018).
Source: Gel, A., Vaidheeswaran, A., Musser, J., and Tong, C. H. (November 22, 2018). “Toward the Development of a Verification, Validation, and Uncertainty Quantification Framework for Granular and Multiphase Flows—Part 1: Screening Study and Sensitivity Analysis.” ASME. J. Verif. Valid. Uncert. September 2018; 3(3): 031001. https://doi.org/10.1115/1.4041745
Verification and Validation (V&V) Studies
Verification attempts to determine whether the equations representing the governing physics are correctly implemented and solved by the computer. On the other hand, validation attempts to answer if the correct equations are being solved by comparing simulation results with a controlled experimental observation at specific validation points [Roache 1997].
In the recent years, there has been a growing emphasis on V&V of MFiX suite, especially with the introduction of MFiX-PIC and MFiX-CGDEM. Each module consists of three main modeling aspects, viz., hydrodynamics, heat and mass transfer and chemical reactions. The current activities involve adopting a comprehensive V&V exercise to cover all these topics. However, there is a shortage of published datasets which have been objectively assessed. Also, most of the experiments reported in the literature lack adequate particle characterization. We follow the roadmap above to design and perform lab-scale experiments after engaging the subject matter experts. We use in-house characterization techniques to assess particle properties before using them in actual physical experiments. This includes advanced instrumentation and optical techniques as discussed in laboratory studies.
The coordinated effort between the modeling and experimental groups has led to great advances in V&V efforts besides aiding our understanding of granular and particle-laden flows (Shahnam et al. 2016, Gel et al. 2017, Vaidheeswaran et al. 2017, Xu et al. 2018, Gel et al. 2018, Bakshi et al. 2018, Fullmer et al. 2018, Xu et al. 2019, Gao et al. 2020, Higham et al. 2020, Vaidheeswaran et al. 2021a, Vaidheeswaran et al. 2021b, Vaidheeswaran et al. 2021c, Higham et el. 2021, Gel et al. 2021a, Gel et al. 2021b, Adepu et al. 2021).
Uncertainty Quantification (UQ) Assessment Studies
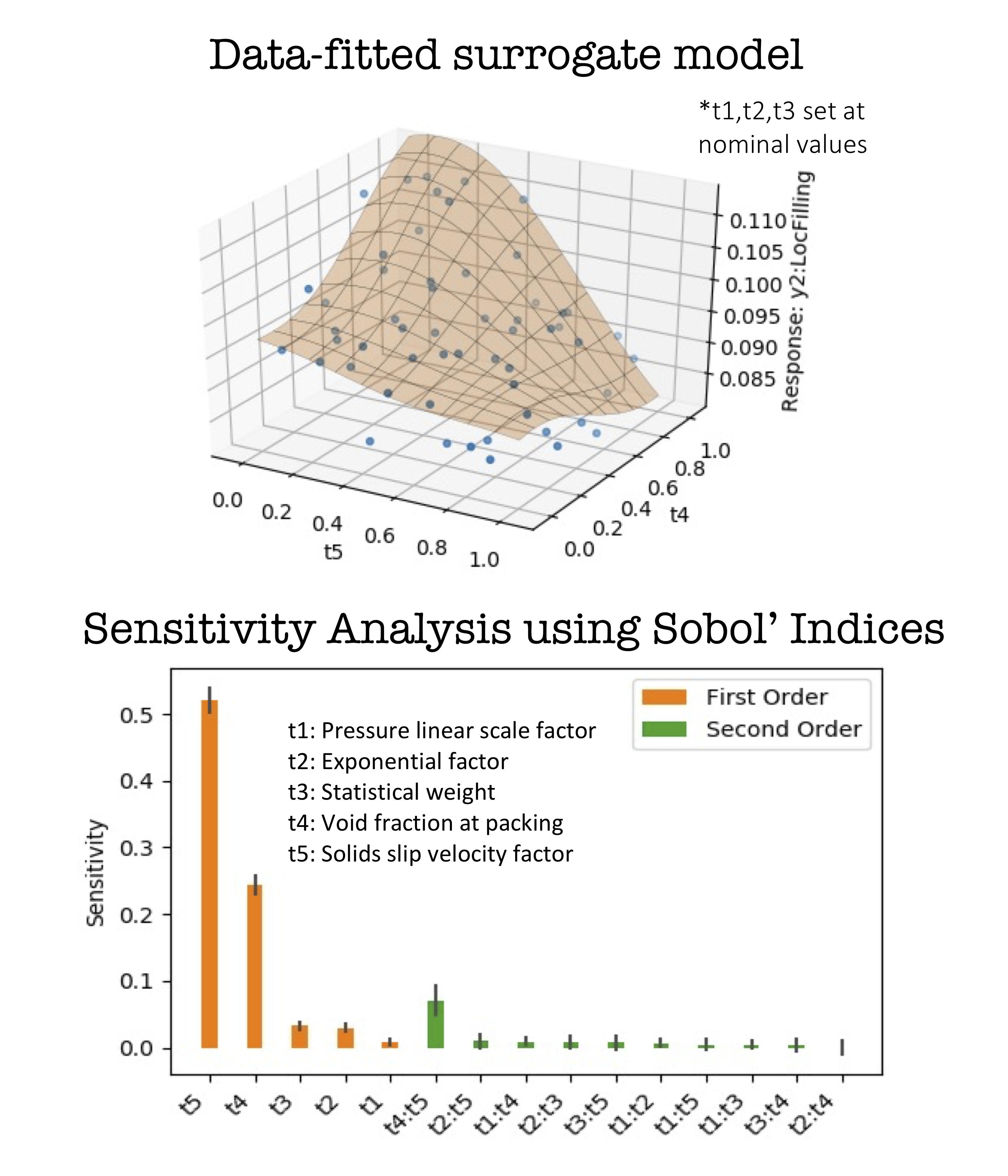
UQ assessment aims to identify, characterize, and propagate various sources of uncertainties in MFiX simulations. One of the critical components of a UQ study is to identify and characterize these uncertainties, which could be due to model parameters, input variables or the inherent assumptions in the model. In addition, the quantities of interest (a.k.a. response variables) are identified to quantify the observed discrepancy. These steps are usually carried out with the feedback from all stakeholders (such as the engineer(s) concerned and subject matter experts). Once a consensus is reached, the uncertainties are characterized as aleatoric, epistemic or mixed. If the number of uncertain variables and parameters are high, sensitivity analysis is employed to assess the dominant ones to narrow down the scope and reduce computational burden. Sensitivity analysis can be also used to plan for follow-up studies. For example, additional physical experiments can be planned to reduce the uncertainties in the select set of model variables, which have been identified to have significant influence. Another UQ study is the forward propagation of the uncertainties, which enables the stakeholders to assess how the quantities of interest are affected and to what extent given the variability in input variables.
Due to the complex governing physics and the nature of computational models, a non-intrusive UQ analysis is preferable and have been adopted in our efforts. In this approach, MFiX solver is treated as a black-box and simulations are performed with the aid of well-established sampling methods (e.g., Optimal Latin Hypercube) in a systematic manner. The variability in the quantities of interest due to input uncertainties are captured using an adequate sampling size. For simulations where the computational cost per sample is high, surrogate model construction (a.k.a. response surface model) is employed to characterize the relationship between the selected set of uncertain input parameters and the quantities of interest. The surrogate models are subsequently used in lieu of the actual simulations in the UQ analysis which requires many function evaluations.
Calibration Studies
Calibration aims to improve the accuracy of MFiX simulations for a given flow configuration by tuning the uncertain model parameters (e.g., heat transfer coefficient in the transient temperature behavior of a fluidized bed simulation) under the guidance of available experimental data. It is important to note the difference between validation and calibration. Validation is a direct comparison of simulation results to experimental data without tuning and is typically employed to establish a baseline comparison between an experiment and a simulation. The identified discrepancy can then justify the need for model calibration. Both validation and calibration are always performed against a specific set of observable data, which makes the credibility of experimental results critical. Hence, careful consideration must be given when generalizing the insights gained from calibration studies, particularly when applying previously calibrated input parameters to new simulations.
Calibration performed for MFiX can be categorized under two methodologies: (i) deterministic, and (ii) statistical. The latter provides a distribution for the calibrated model parameters instead of single values, which is the outcome of deterministic calibration. Another major difference is the ability of statistical calibration to take into account model bias (a.k.a. model form uncertainty) while calibrating input model parameters.