5.1. PIC01: Terminal velocity

5.1.1. Description

This case is similar to “DEM06: Single particle, terminal velocity”. A computational parcel containing physical particles is subjected to a uniform gas velocity. The statistical weight and initial gas volume fraction are adjusted such that all particles are accommodated in one parcel for the given grid resolution. The simulation results are compared with the analytical results obtained by solving the following system of Ordinary Differential Equations:

(5.1)\[\frac{d^{2}y}{dt^{2}} = \frac{d v_{p}}{dt} = \frac{g (\rho_{p}-\rho_{g})}{\rho_{p}}-\frac{3}{4} C_{d} \frac{\rho_{g}|v_{p}-v_{g}|^{2}}{\rho_{p} d_{p}}\]

The initial and boundary conditions are given by,

(5.2)\[y(0) = h_{0};\quad \frac{d y}{dt} (0) = 0\]

where, \(y\) is the position of particle center measured from the bottom wall, \(v_{p}\) and \(v_{g}\) are the particle and gas velocities, \(\rho_{p}\) and \(\rho_{g}\) are particle and gas densities, \(d_{p}\) is the particle diameter, \(h_{0}\) is the initial height of the particle, \(g\) is the acceleration due to gravity, and \(C_{d}\) is the drag coefficient. In this case, \(C_{d}=1\) is used for simplicity. The effect of the parcel on the gas phase is neglected since particle concentration is extremely dilute. Hence, the momentum equations for the gas-phase are not solved.

5.1.2. Setup

Table 5.2 PIC-01 Setup, Initial and Boundary Conditions.

Computational/Physical model

3D, Transient

Multiphase

Gravity

Thermal energy equation is not solved

Turbulence equations are not solved (Laminar)

Uniform mesh

First order upqind discritization scheme

Geometry

Coordinate system

Cartesian

Grid partitions

x-length

0.01

(m)

5

y-length

0.30

(m)

60

z-length

0.01

(m)

5

Material

Gas density, \(\rho_{g}\)

1.2

(kg·m-3)

Gas viscosity, \(\mu_{g}\)

1.8E-05

(Pa·s)

Solids Type

PIC

Diameter, \(d_{p}\)

0.1

(m)

Density, \(\rho_{s}\)

2000

(kg·m-3)

Solids Properties (PIC)

Pressure linear scale factor, \(P_{s}\)

100.0

(Pa)

Exponential scale factor, \(\gamma\)

3.0

(-)

Statistical weight

100

(-)

Initial Conditions

x-velocity, \(u_{g}\)

0.0

(m·s-1)

y-velocity, \(v_{g}\)

0.4

(m·s-1)

z-velocity, \(w_{g}\)

0.0

(m·s-1)

Solids concentration, \(\epsilon_{s}\)

0.0001

(-)

Gas volume fraction at packing, \(\epsilon_{g}^{*}\)

0.4

(-)

Pressure, \(P_{g}\)

101,325

(Pa)

Boundary Conditions

South

0.4

(m·s-1)

Mass inflow

North

101,325

(Pa)

Pressure outflow

West, east, top and bottom

Free-Slip wall

5.1.3. Results

As the parcel falls, its velocity increases initially, and reaches its terminal velocity when the gravitational force is balanced by the drag force. The numerical solution to the system of equations is obtained using \(4^{th}\) order Runge-Kutta method. The values are compared with the MFiX-PIC simulations as shown in Fig. 5.1. The velocity and position are accurately predicted by MFiX-PIC as was the case with MFiX-DEM.

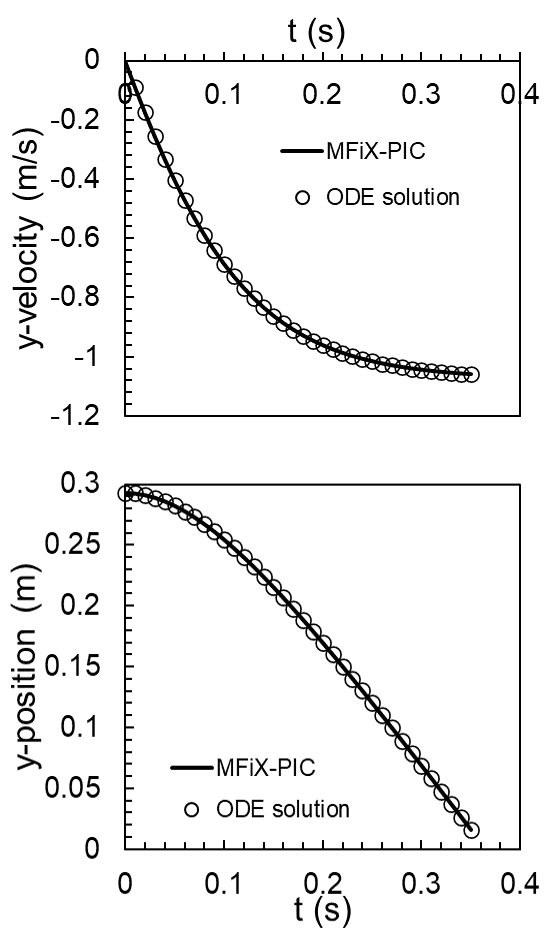
../_images/pic01-1.png

Fig. 5.1 Predictions using MFiX-PIC: velocity (top) and position (bottom).