5.7. PIC07: Minimum fluidization

5.7.1. Description

A minimum fluidization test is used to validate the interphase momentum transfer between gas and particles. In contrast to particles settling in a quiescent fluid medium described in the case PIC, a gas phase enters the domain through the bottom boundary, initially through a fixed bed of particles. Once the minimum fluidization condition is reached, the particles change from a fixed state to a fluidized state. This action is accompanied by a change in pressure drop across the bed. The physical experiments were performed at NETL using high-density polyethylene (HDPE) particles in a rectangular domain (0.05 m X 0.20 m X 0.05 m). The mean diameter and density of HDPE are 870 \(\mu m\) and 860 \(kg·m^{-3}\). Figure Fig. 5.9 shows the plot of pressure drop as a function of gas velocity, where the pressure drop is normalized by the weight of bed given by,

(5.12)\[\Delta P* = \frac{\Delta P}{\frac{m g}{A}}\]

where \(\Delta P\) is the pressure drop across the bed, g is the mass of bed material, \(g\) is acceleration due to gravity and \(A\) is the cross-sectional area of the bed. There is a sharp transition between fixed and fluidized states which marks the minimum fluidization condition. The graphical abscissa at this transition is recognized as the minimum fluidization velocity and the ordinate is the pressure drop that corresponds to the weight of bed material. Based on linear fit between the two regions, minimum fluidization velocity for the case shown is 0.182 \(m/s\).

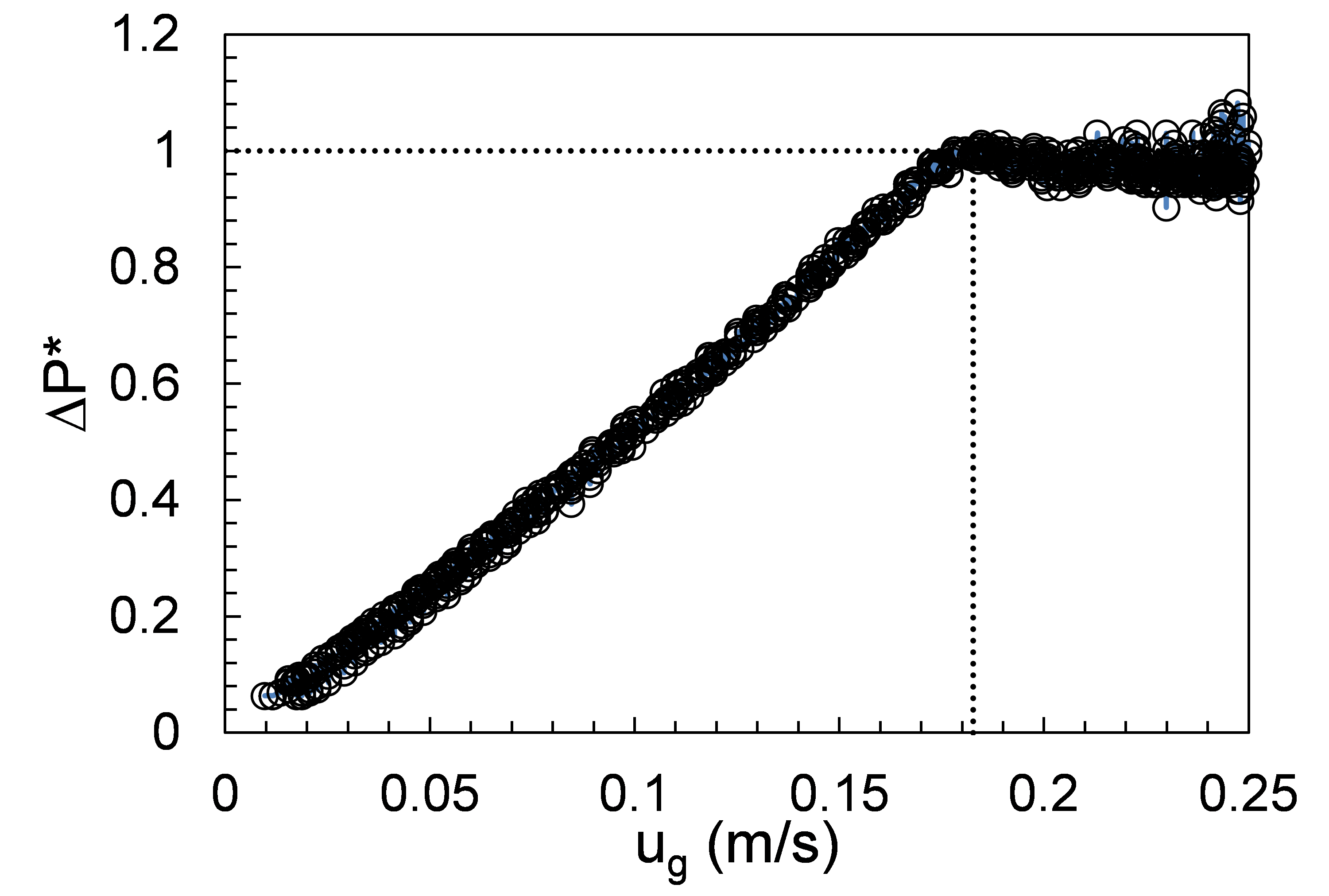
../_images/pic07-1.png

Fig. 5.9 Normalized pressure drop as a function of inlet gas velocity.

Considering the size of particles, it was decided to use a larger domain which could accommodate more computational parcels. Hence, this study used a rectangular domain (0.10 m X 0.40 m X 0.10 m). The drag correlation of Wen and Yu [3] is used for calculating the drag coefficient \(\beta\) given by,

(5.13)\[\begin{split}C_{d} = \begin{cases} \frac{24}{Re} (1 + 0.15 Re^{0.687}) & Re \leq 1000 \\ 0.44 & Re > 1000 \end{cases}\end{split}\]

The particle’s Reynolds number is defined as,

(5.14)\[Re = \frac{\rho_{g} \epsilon_{g} |u_{g}-u_{s}| d_{p}}{\mu_{g}}\]

where, \(\rho_{g}, \epsilon_{g}, u_{g}, \mu_{g}\) represent density, volume fraction, velocity, and dynamic viscosity of the gas phase. \(u_{s}, d_{p}\) are the velocity and diameter of particles in the solids phase (Note: \(d_p\) is the diameter of particle and not parcel).

5.7.2. Setup

Table 5.14 PIC-07 Setup, Initial and Boundary Conditions.

Computational/Physical model

3D, Transient

Multiphase

Gravity

Thermal energy equation is not solved

Turbulence equations are not solved (Laminar)

Uniform mesh

First order upwind discritization scheme

Geometry

Coordinate system

Cartesian

Grid partitions

x-length

0.10

(m)

10

y-length

0.40

(m)

40

z-length

0.10

(m)

10

Material

Gas density, \(\rho_{g}\)

1.0

(kg·m-3)

Gas viscosity, \(\mu_{g}\)

1.8E-5

(Pa·s)

Solids Type

PIC

Diameter, \(d_{p}\)

0.87

(mm)

Density, \(\rho_{s}\)

860.0

(kg·m-3)

Solids Properties (PIC)

Pressure linear scale factor, \(P_{s}\)

1.0

(Pa)

Exponential scale factor, \(\gamma\)

4.0

(-)

Statistical weight

4.0,5.0,10.0

(-)

Gas volume fraction at packing, \(\epsilon_{g}^{*}\)

0.44

(-)

Initial Conditions

x-velocity, \(u_{g}\)

0.0

(m·s-1)

y-velocity, \(v_{g}\)

0.0

(m·s-1)

z-velocity, \(w_{g}\)

0.0

(m·s-1)

Gas volume fraction, \(\epsilon_{g}\)

0.82

(-)

Pressure, \(P_{g}\)

101,325

(Pa)

Boundary Conditions

South boundary, \(u_{g}\)

Varied

(m·s-1)

Mass inflow

North boundary, \(P_{g}\)

101,325

(Pa)

Pressue outflow

All other boundaries

No-slip walls

5.7.3. Results

Time-dependent boundary velocity for the gas-phase is specified through a user-defined subroutine. A linear ramp function is used, and pressure drop across the bed is extracted at regular intervals. It is worth reiterating that the domain considered for this numerical exercise is different from physical experiments, hence this study does not to show the experimental curve in the resulting plots. However, minimum fluidization is expected to be the same barring minor differences due to factors including wall effects. The transition between fixed and fluidized states is not distinctly predicted by MFiX-PIC Fig. 5.10 as observed in the experiments. MFiX-PIC does not reproduce the behavior of HDPE particles at minimum fluidization velocity. This could be due to the nature of the particle-stress closure or uncertainty in model parameters. This could also point to a limitation of MFiX-PIC in modeling the fluidization transition from a fixed bed state. However, PIC is capable of predicting the pressure drop corresponding to the weight of bed material, further away from minimum fluidization conditions. Fig. 5.10 also highlights the negligible effect of parcel size for this case. Sensitivity of \(\epsilon^{*}\) and \(P_{s}\) are also analyzed. For the range of \(P_{s}\) considered in this study, the behavior is unchanged for all practical purposes as observed in Fig. 5.11. However, as \(\epsilon^{*}\) changed there is a noticeable difference in the fluidization behavior Fig. 5.12. Maximum sensitivity was observed for \(\epsilon^{*}\) among other parameters considered in this study. A more systematic approach as outlined in Gel et al. [9] is required to draw further conclusions on the observed behavior.

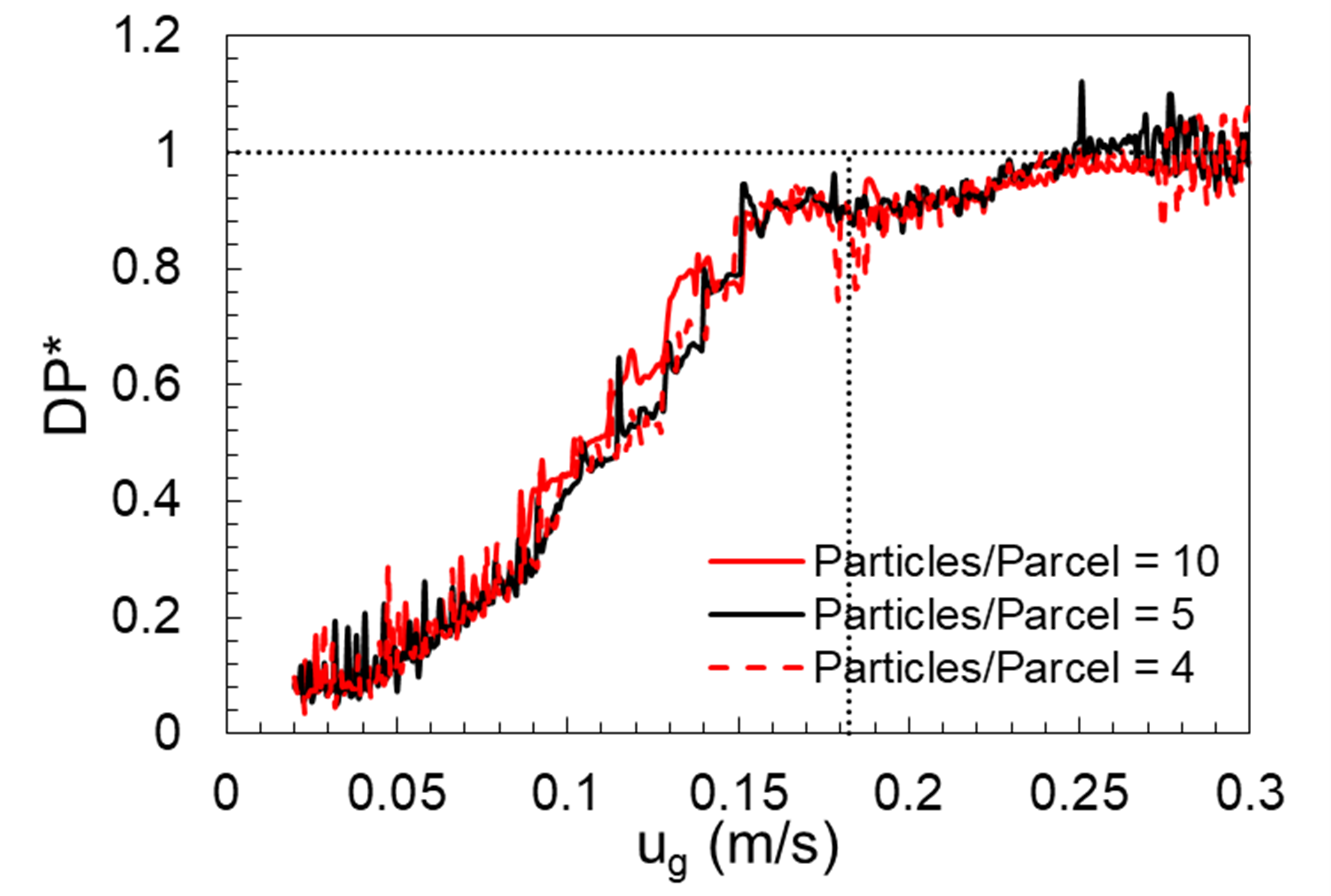
../_images/pic07-2.png

Fig. 5.10 Effect of statistical weight (particles per parcel) on fluidization curve using MFiX-PIC.

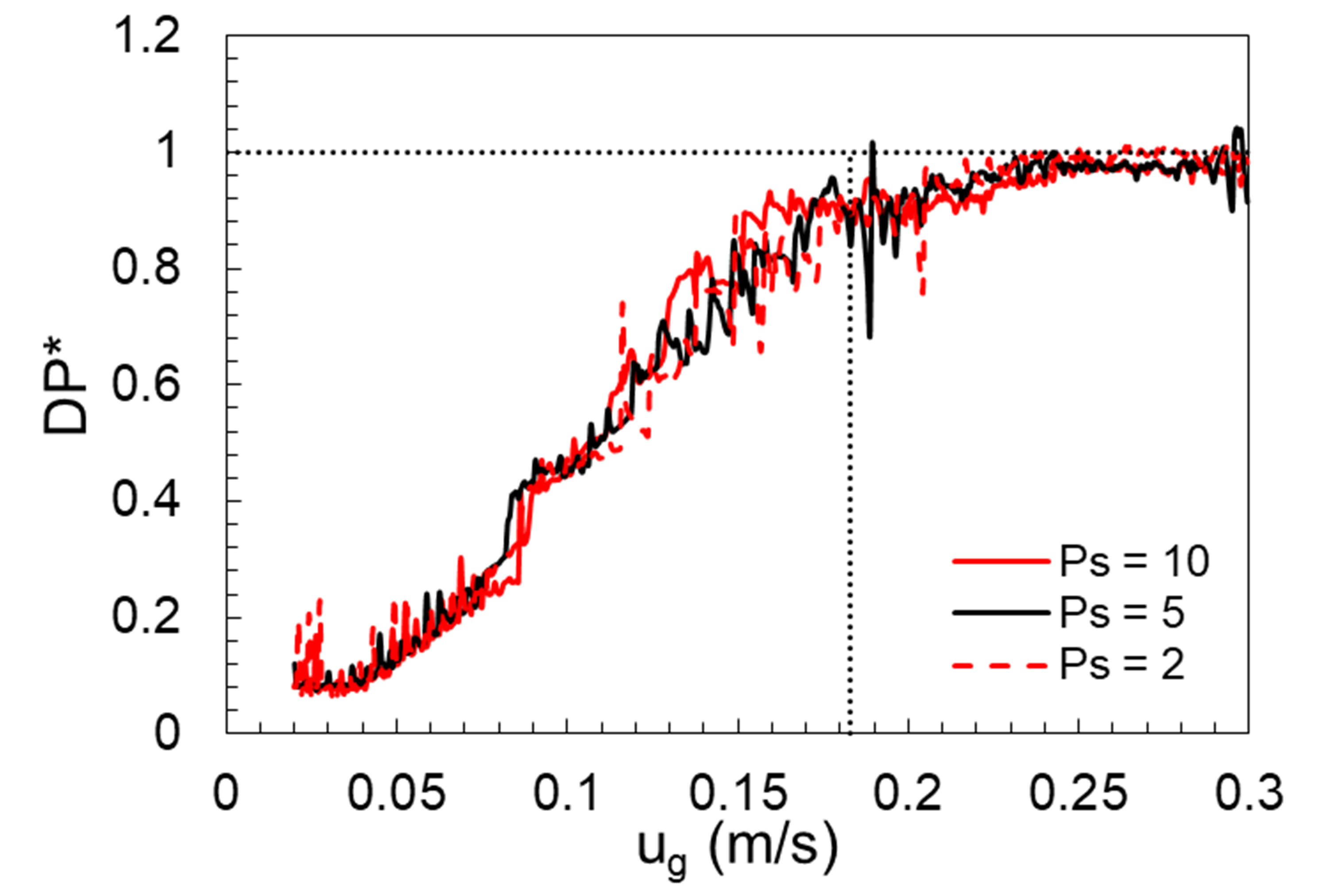
../_images/pic07-3.png

Fig. 5.11 Effect of varying \(P_{s}\).

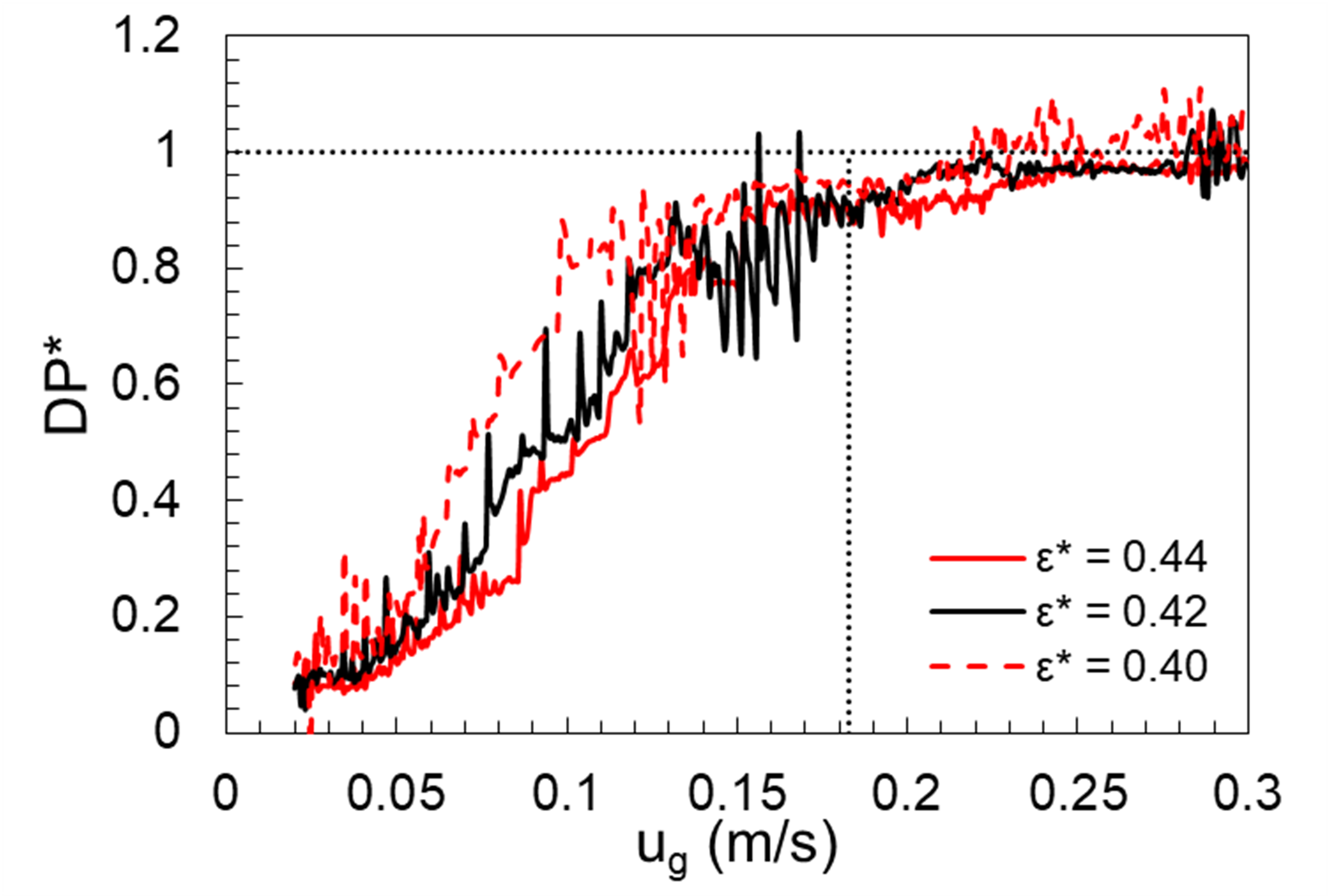
../_images/pic07-4.png

Fig. 5.12 Effect of varying gas volume fraction at packing \(\epsilon_{g}^*\).