3.3. FLD03: Steady, lid-driven square cavity¶
3.3.1. Description¶
Lid-driven flow in a 2D square cavity in the absence of gravity is illustrated in Fig. 3.6. The problem definition follows the work of Ghia et al. [10] where the domain is bounded on three sides with stationary walls while one wall, the lid, is prescribed a constant velocity. The cavity is completely filled with a fluid of selected viscosity and the flow is assumed to be incompressible and laminar.

Fig. 3.6 Schematic of the lid-driven square cavity.¶
3.3.2. Setup¶
########################################################################
# #
# Author: M. Syamlal Date: Dec 1999 #
# Revised: A. Choudhary and J. Musser Date: Jun 2015 #
# #
# A top wall driven cavity with only fluid phase present in the #
# absence of gravitational forces. #
# #
# REF: Ghia U., Ghia K.N., and Shin C.T., High-Re Solutions for Incom- #
# pressible Flow Using the Navier-Stokes Equations and a Multi- #
# grid Method, Journal of Computational Physics, Volume 48, pages #
# 387-411, 1982. doi: 10.1016/0021-9991(82)90058-4 #
# #
########################################################################
RUN_NAME = 'FLD03'
DESCRIPTION = 'Lid-driven cavity'
#_______________________________________________________________________
# RUN CONTROL SECTION
UNITS = 'SI'
RUN_TYPE = 'NEW'
TSTOP = 1.0d8
DT = 1.0e-2
DT_FAC = 1.0
ENERGY_EQ = .F.
SPECIES_EQ(0) = .F.
GRAVITY = 0.0
CALL_USR = .T.
#_______________________________________________________________________
# NUMERICAL SECTION
LEQ_PC(1:9) = 9*'DIAG'
DISCRETIZE(1:9) = 9*2
DETECT_STALL = .F.
NORM_G = 1.0
#_______________________________________________________________________
# GEOMETRY SECTION
COORDINATES = 'CARTESIAN'
ZLENGTH = 1.0 NO_K = .T.
XLENGTH = 1.0 IMAX = 128
YLENGTH = 1.0 JMAX = 128
#_______________________________________________________________________
# GAS-PHASE SECTION
RO_G0 = 1.0 ! (kg/m3)
MU_G0 = 0.01 ! (Pa.sec)
#_______________________________________________________________________
# SOLIDS-PHASE SECTION
MMAX = 0
#_______________________________________________________________________
# INITIAL CONDITIONS SECTION
IC_X_w(1) = 0.00 ! (m)
IC_X_e(1) = 1.00 ! (m)
IC_Y_s(1) = 0.00 ! (m)
IC_Y_n(1) = 1.00 ! (m)
IC_EP_g(1) = 1.00
IC_U_g(1) = -1.0e-2! (m/sec)
IC_V_g(1) = 0.00 ! (m/sec)
#_______________________________________________________________________
# BOUNDARY CONDITIONS SECTION
! West, East and South are default No-Slip Walls (NSW)
! North: Lid with a constant velocity of 1.0 m/s along +x using a
! partial slip wall (PSW) implemented as dv/dn + Hw(V-Vw) = 0.0
! where Vw is the wall speed and Hw is undefined (Inf).
!---------------------------------------------------------------------//
BC_X_w(1) = 0.00 ! (m)
BC_X_e(1) = 1.00 ! (m)
BC_Y_s(1) = 1.00 ! (m)
BC_Y_n(1) = 1.00 ! (m)
BC_TYPE(1) = 'PSW'
BC_Uw_g(1) = 1.00 ! (m/sec)
BC_Vw_g(1) = 0.00 ! (m/sec)
#_______________________________________________________________________
# OUTPUT CONTROL SECTION
RES_DT = 5.0d3 ! (sec)
SPX_DT(1:9) = 9*5.0d3 ! (sec)
FULL_LOG = .F.
RESID_STRING = 'P0' 'U0' 'V0'
#_______________________________________________________________________
# DMP SETUP
! NODESI = 1 NODESJ = 1 NODESK = 1
3.3.3. Results¶
Numerical solutions were obtained on a 128x128 grid mesh for Reynolds numbers of 100 and 400 by specifying fluid viscosities of 1/100 and 1/400 Pa·s, respectively. A time step of 0.01 second was used and the simulations considered converged when the average L2 Norms for the x-axis and y-axis velocity components, \(u_{g}\) and \(v_{g}\), were less than 10-8.
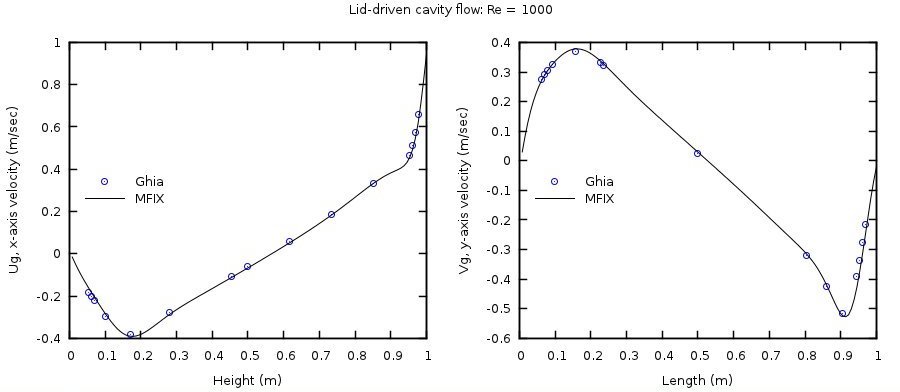
The horizontal velocity at the vertical centerline (\(x = 0.5\)) and the vertical velocity at the horizontal centerline (\(y = 0.5\)) are compared with those of Ghia et al. [10] in Fig. 3.7 and Fig. 3.8.
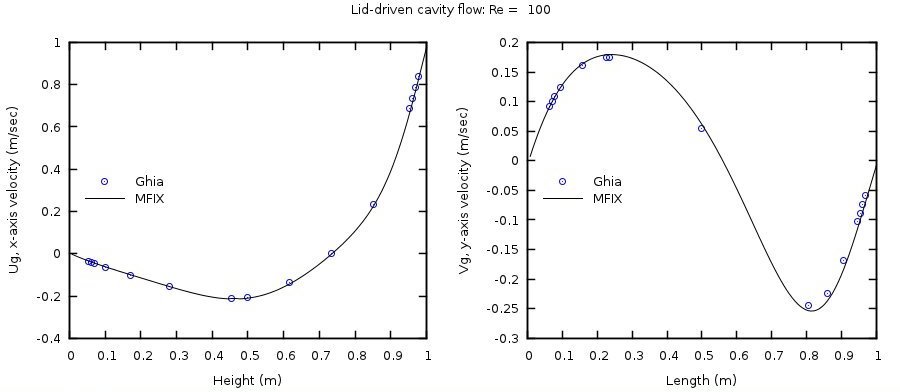
Fig. 3.7 Comparison of velocities at the vertical (x=0.5) and horizontal centerlines (y=0.5) of the cavity with Ghia et al. [10] for Reynolds number of 100 (128x128 grid).¶
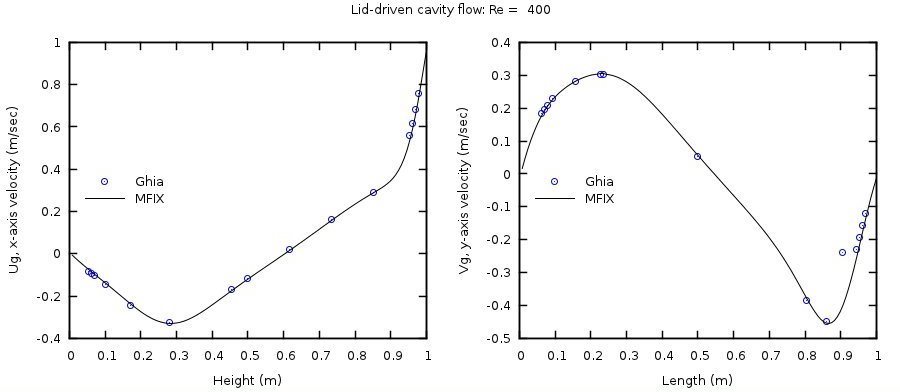
Fig. 3.8 Comparison of velocities at the vertical (x=0.5) and horizontal centerlines (y=0.5) of the cavity with Ghia et al. [10] for Reynolds number of 400 (128x128 grid).¶
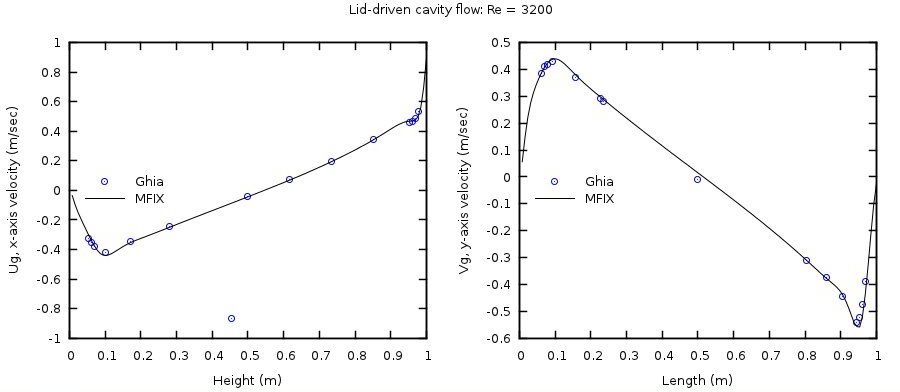
Similarly, numerical solutions were obtained on a 128x128 grid mesh for Reynolds numbers of 1000 and 3200 by specifying fluid viscosities of 1/1000 and 1/3200 Pa·s, respectively. The horizontal velocity at the vertical centerline (\(x = 0.5\)) and the vertical velocity at the horizontal centerline (\(y = 0.5\)) are compared with those of Ghia et al. [10] in Fig. 3.9 and Fig. 3.10. These cases are not included in the continuous integration server test suite.