3.7. FLD07: Steady, 2D fully-developed, turbulent channel flow¶
3.7.1. Description¶
This case uses 2D, fully-developed turbulent channel flow between two horizontal, parallel plates separated by a width, \(W\), to assess the single phase k-ϵ model in MFIX. Periodic boundaries with a specified pressure drop are imposed in the y-direction as shown in Fig. 3.18.

Fig. 3.18 Turbulent flow in a 2D channel¶
The pressure drop along the channel is equated to the shear stress at the walls, \(\tau_{w}\).
The shear stress is related to the gas density, \(\rho_{g}\), and friction velocity, \(v_{*}\),
where, the friction velocity, is given by the Reynolds number.
3.7.2. Setup¶
#########################################################################
# #
# Author: Avinash Vaidheeswaran Date: July 2016 #
# Turbulent flow in a pipe problem: #
# #
# Turbulent flow through a channel is simulated and the results are #
# compared with the data from DNS #
# #
#########################################################################
RUN_NAME = 'FLD07'
DESCRIPTION = 'Turbulent channel flow'
#_______________________________________________________________________
# RUN CONTROL SECTION
UNITS = 'SI'
RUN_TYPE = 'NEW'
TSTOP = 1.0d8
DT = 0.02
ENERGY_EQ = .F.
SPECIES_EQ(0) = .F.
GRAVITY = 0.0
CALL_USR = .T.
#_______________________________________________________________________
# NUMERICAL SECTION
DISCRETIZE(1:9) = 9*2
NORM_g = 0.0
#_______________________________________________________________________
# GEOMETRY SECTION
COORDINATES = 'CARTESIAN'
ZLENGTH = 1.00 NO_K = .T.
XLENGTH = 2.00 IMAX = 8
YLENGTH = 1.00 JMAX = 4
#_______________________________________________________________________
# GAS-PHASE SECTION
RO_g0 = 1.0 ! (kg/m3)
MU_g0 = 1.0d-04 ! (Pa.s)
TURBULENCE_MODEL = 'K_EPSILON'
MU_GMAX = 1.0d6 ! (Pa.s)
#_______________________________________________________________________
# SOLIDS-PHASE SECTION
MMAX = 0
#_______________________________________________________________________
# INITIAL CONDITIONS SECTION
IC_X_w(1) = 0.0 ! (m)
IC_X_e(1) = 2.0 ! (m)
IC_Y_s(1) = 0.0 ! (m)
IC_Y_n(1) = 1.0 ! (m)
IC_EP_G(1) = 1.0
IC_P_G(1) = 0.0 ! (Pa)
IC_U_G(1) = 1.0d-6 ! (m/sec)
IC_V_G(1) = 1.0 ! (m/sec)
IC_K_TURB_G(1) = 0.010 ! (m2/s2)
IC_E_TURB_G(1) = 0.001 ! (m2/s3)
#_______________________________________________________________________
# BOUNDARY CONDITIONS SECTION
! Flow boundaries: Periodic with specified pressure drop
!---------------------------------------------------------------------//
CYCLIC_Y_PD = .T.
DELP_Y = @(0.0543496*0.0543496) ! (Pa)
! The east and west boundaries are no-slip walls (NSW)
!---------------------------------------------------------------------//
BC_X_w(1:2) = 0.0 2.0 ! (m)
BC_X_e(1:2) = 0.0 2.0 ! (m)
BC_Y_s(1:2) = 0.0 0.0 ! (m)
BC_Y_n(1:2) = 1.0 1.0 ! (m)
BC_TYPE(1:2) = 2*'NSW'
#_______________________________________________________________________
# OUTPUT CONTROL SECTION
RES_DT = 1.0d6
SPX_DT(1:9) = 9*1.0
FULL_LOG = .F.
RESID_STRING = 'P0' 'U0' 'V0' 'K0'
#_______________________________________________________________________
# DMP SETUP
! NODESI = 1 NODESJ = 2 NODESK = 1
3.7.3. Results¶
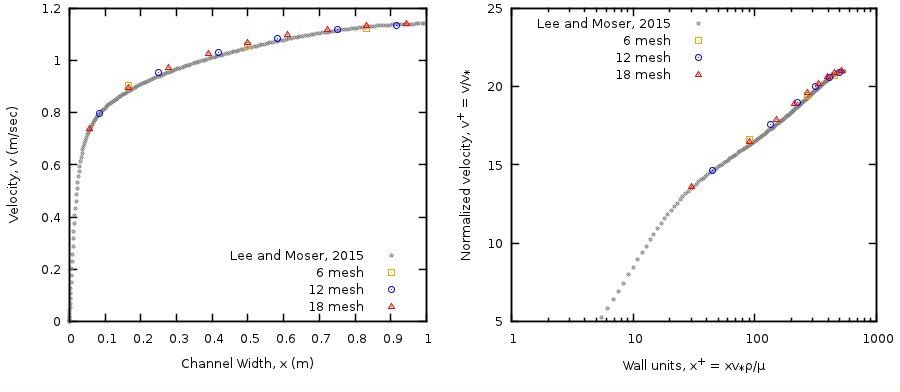
The pressure drop in the y-axial direction, domain length and width, and gas density were chosen to reflect the conditions of Lee and Moser [14] for \(\text{Re}_{\tau} = 543\). The DNS dataset was accessed on November 10, 2016 from http://turbulence.ices.utexas.edu/channel2015/data/LM_Channel_0550_mean_prof.dat.
Transient simulations were performed for better numerical stability. The solution was considered converged when the L2 norms for the gas velocity components, \(u_{g}\) and \(v_{g}\), turbulent kinetic energy, \(k_{g}\), and rate of turbulent kinetic energy dissipation, \(\epsilon_{g}\), were all less than 10-10.
Simulations were conducted for three mesh levels [6, 12, 18] in the x-axial direction. Mesh levels were selected to ensure that the stream-ways velocity components in computational cells adjacent to the wall were located outside the buffer layer. Specifically, the first stream-ways velocity component should be located at least 30 wall units from the wall to be consistent with the \(k - \epsilon\) model wall function implementation.
The MFIX results are shown in Fig. 3.19 along with the direct numerical simulation (DNS) data of Lee and Moser [14] for \(\text{Re}_{\tau} = 543\). The velocity profiles for the three mesh levels are shown on the left whereas the normalized velocity profiles with respect to wall units are shown on the right.