2.7. MMS03: Two-phase, 3D, curl-based functions with variable volume fraction¶
2.7.1. Description¶
The volume fraction is selected as a function with sufficient variation in all directions while ensuring that the packed bed volume fraction (\(\varepsilon_{g} = 0.42\)) is not reached. The velocity manufactured solutions are now selected to satisfy the continuity equations (not divergence-free velocity conditions as in Section 2.6). The resulting manufactured solutions for gas volume fraction and fluid velocity variables are shown in Fig. 2.14. The mathematical form of the manufactured solutions is discussed in Section 6.
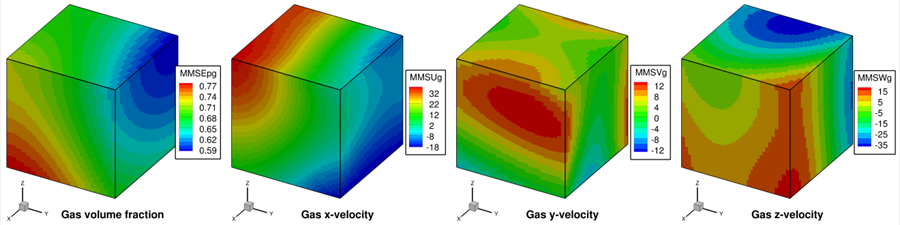
Fig. 2.14 Manufactured solutions for 3D, variable volume fraction, two-phase verification.¶
2.7.2. Setup¶
Computational/Physical model |
||
|---|---|---|
3D, Steady-state, incompressible |
||
Two-phase |
||
No gravity |
||
Drag model is turned off |
||
Friction model is turned off |
||
Thermal energy equations are solved |
||
Granular energy equation is not solved |
||
Turbulence equations are not solved (Laminar) |
||
Non-uniform mesh |
||
Central scheme |
||
Geometry |
||
Coordinate system |
Cartesian |
|
Domain length, \(L\) (x) |
1.0 |
(m) |
Domain height, \(H\) (y) |
1.0 |
(m) |
Domain width, \(W\) (z) |
1.0 |
(m) |
Material † |
||
Fluid density, \(\rho_{g}\) |
1.0 |
(kg·m-3) |
Fluid viscosity, \(\mu_{g}\) |
1.0 |
(Pa·s) |
Fluid specific heat, \(C_{\text{pg}}\) |
0.05 |
(J·kg-1·K-1) |
Fluid thermal conductivity, \(k_{g}\) |
1.0 |
(J·kg-1·K-1·s-1) |
Solids density, \(\rho_{s}\) |
2.0 |
(kg·m-3) |
Solids viscosity, \(\mu_{s}\) |
2.0 |
(Pa·s) |
Solids specific heat, \(C_{\text{ps}}\) |
0.1 |
(J·kg-1·K-1) |
Solids thermal conductivity, \(k_{s}\) |
2.0 |
(J·kg-1·K-1·s-1) |
Initial Conditions |
||
Pressure (gauge), \(P_{g}\) |
0.0 |
(Pa) |
Fluid x-velocity, \(u_{g}\) |
10.0 |
(m·s-1) |
Fluid y-velocity, \(v_{g}\) |
10.0 |
(m·s-1) |
Fluid z-velocity, \(w_{g}\) |
10.0 |
(m·s-1) |
Solids x-velocity, \(u_{s}\) |
5.0 |
(m·s-1) |
Solids y-velocity, \(v_{s}\) |
5.0 |
(m·s-1) |
Solids z-velocity, \(w_{s}\) |
5.0 |
(m·s-1) |
Fluid temperature, \(T_{g}\) |
350.0 |
(K) |
Solids temperature, \(T_{s}\) |
300.0 |
(K) |
Gas volume fraction, \(\varepsilon_{g}\) |
MMS |
– |
Boundary Conditions ‡ |
||
All boundaries |
Mass inflow |
† Material properties selected to ensure comparable contribution from convection and diffusion terms. Specified values are constant to avoid the introduction of constitutive laws.
‡ The manufactured solution is imposed on all boundaries (i.e., Dirichlet specification).
2.7.3. Results¶
Numerical solutions were obtained using the Central discretization scheme for 8x8, 16x16, 32x32, 64x64, and 128x128 grid meshes. Iterative convergence was not achieved when continuity equations were solved with a variable volume fraction field. To achieve convergence, the continuity variables (\(\varepsilon_{g}\), \(\rho_{g}^{'}\), and \(P_{g}\)) were kept fixed by specifying the fields for these variables using the manufactured solution in the initial conditions routine, and discarding their iterative solution within the main solver routine. Thus, the continuity and pressure equations were not solved in this case. This restricts the ability to make any observations about the accuracy of these equations. The observed order of accuracy matches the formal order as shown in Fig. 2.15 for both velocity and energy variables.
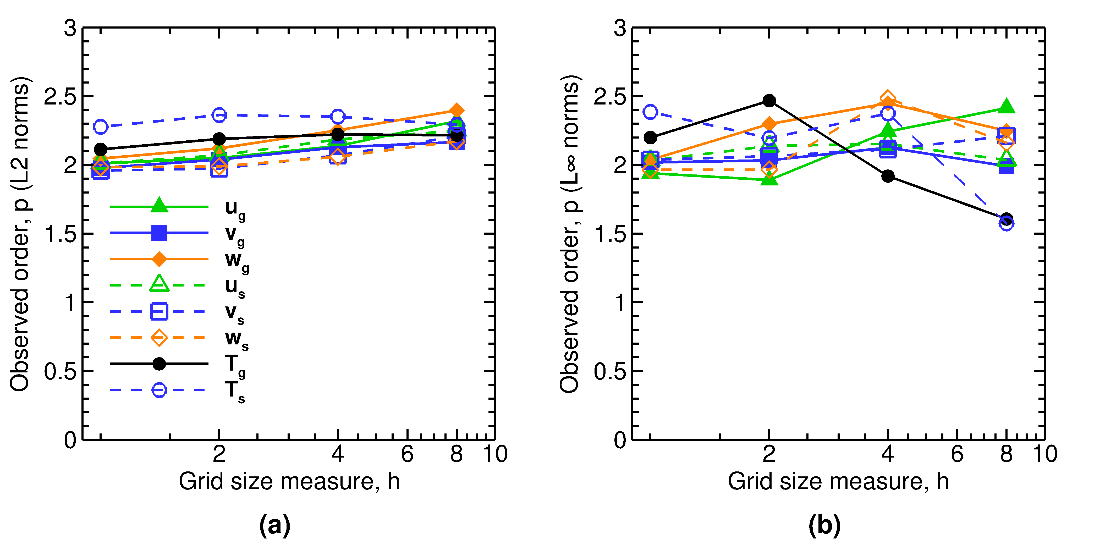
Fig. 2.15 Observed orders of accuracy for 3D, two-phase flows (variable volume fraction) using (a) \(\mathbf{L}_{\mathbf{2}}\) norms, and (b) \(\mathbf{L}_{\mathbf{\infty}}\) norms of the discretization error.¶