2.1. MMS Procedure Overview

To better instruct the reader, the procedure for using a MMS to conduct an order of accuracy test is summarized by example [26][19] :

1. Allow any partial differential equation in n-dimensions to be represented through the notation:

(2.1)\[L\left\lbrack u\left( x_{1},x_{2},\cdots,x_{n},t \right) \right\rbrack = 0\]

For example, a one-dimensional non-linear Burger equation:

(2.2)\[u_{t} + uu_{x} = \alpha u_{\text{xx}}\]

would be represented as:

(2.3)\[L\left\lbrack u\left( x,t \right) \right\rbrack = u_{t} + uu_{x} - \alpha u_{\text{xx}} = 0\]

2. Make up a manufactured solution to the proposed partial differential equation. The chosen solution does not need to represent the solution to a physical problem. The MMS is a mathematical exercise to determine if a piece of software will accurately calculate a solution to its prescribed numerical order.

   For example, allow: \(U\left( x,t \right) = A + sin\left( x + Ct \right)\) where \(A\) and \(C\) are constants, to be a solution to \(L\left\lbrack u\left( x,t \right) \right\rbrack\).

   The key is that whatever one chooses for \(U\left( x,t \right)\), it must be mathematically analytic, meaning fully differentiable with continuous derivatives to at least the order of the partial differential equation one is trying to solve over the full domain of the problem. In this example, the constant value function \(A\) and the sinusoidal function \(sin\left( x + Ct \right)\) obviously meet these criteria. Do not choose functions that display discontinuities of any type for any derivative if the domain of interest extends through those discontinuities. In addition, it is important that all terms in a given manufactured solution are of similar magnitude. This assures that solutions are not dominated by a single term which might skew order of accuracy results.

   It is essential to choose solutions that do not engage physical constraints within the code that is under evaluation. For example, MFIX issues an error message and stops all calculations if the temperature in any computational cell falls below 250 Kelvin. So, if testing the energy equation, the manufactured solution should never present a value less than 250, as this value is contextually interpreted as an unphysical temperature.

3. Apply the manufactured solution to the partial differential equation being solved. This means create the derivatives represented in the original problem and substitute them into the equation.

   For example, using \(U\left( x,t \right) = A + sin\left( x + Ct \right)\) as a manufactured solution for \(L\left\lbrack u\left( x,t \right) \right\rbrack = u_{t} + uu_{x} - \alpha u_{\text{xx}} = 0\) requires

(2.4)\[L\left\lbrack u\left( x,t \right) \right\rbrack_{U\left( x,t \right)} = \frac{\partial}{\partial t}\left( U\left( x,t \right) \right) + U\left( x,t \right)\frac{\partial}{\partial x}\left( U\left( x,t \right) \right) - \alpha\frac{\partial^{2}}{\partial x^{2}}\left( U\left( x,t \right) \right) = 0\]

After substitution,

(2.5)\[L\left\lbrack u\left( x,t \right) \right\rbrack_{U\left( x,t \right)} = C\cos{\left( x + Ct \right) + \left( A + \sin\left( x + Ct \right) \right)\left( \cos\left( x + Ct \right) \right) - \alpha\left( - \sin\left( x + Ct \right) \right)} = 0\]

Or,

(2.6)\[L\left\lbrack u\left( x,t \right) \right\rbrack_{U\left( x,t \right)} = \left( A + C \right)\cos{\left( x + Ct \right) + \sin{\left( x + Ct \right)\cos\left( x + Ct \right)} + \alpha\sin\left( x + Ct \right)} = 0\]

\(L\left\lbrack u\left( x,t \right) \right\rbrack_{U\left( x,t \right)}\) represents what are called source terms in MMS. Thinking about this using notation:

(2.7)\[L\left\lbrack u\left( x,t \right) \right\rbrack = 0 = L\left\lbrack u\left( x,t \right) \right\rbrack_{U\left( x,t \right)}\]

Or,

(2.8)\[L\left\lbrack u\left( x,t \right) \right\rbrack - L\left\lbrack u\left( x,t \right) \right\rbrack_{U\left( x,t \right)} = 0\]

After calculation, any arithmetic difference between the numerical solution and the exact solution is assumed to originate from the numerical method.

4. To properly solve a partial differential equation of the form \(L\left\lbrack u\left( x_{1},x_{2},\cdots,x_{n},t \right) \right\rbrack = 0\), one needs appropriately chosen initial and boundary values.

   So, by example, assume that the physical domain of interest is \(\text{xϵ}\left\lbrack 0,1 \right\rbrack\) and allow \(\text{tϵ}\left\lbrack 0, \right.\ \left. \ \infty \right)\).

   First, force the initial condition of \(u\left( x,0 \right)\) to align with that of the manufactured solution, \(U\left( x,0 \right)\) by choosing,

(2.9)\[u\left( x,0 \right) = U\left( x,0 \right) = A + \sin\left( x + C\left( 0 \right) \right) = A + sin\left( x \right)\]

Then, select boundary conditions in any meaningful way, forcing alignment between the proposed partial differential equation and the manufactured solution. For example, perhaps fixed boundary conditions are useful. These are sometimes called Dirichlet boundary conditions. Applying a fixed boundary condition means choose functions for fixed boundary locations that will be maintained through all time-steps. It does not mean that a boundary must have the same value for all time, although that is a possibility (the function chosen might be a constant).

So, for this example, an appropriate fixed boundary condition would be:

(2.10)\[\begin{split}\begin{matrix} u\left( 0,t \right) = U\left( 0,t \right) = A + \sin\left( 0 + Ct \right) = A + \sin\left( \text{Ct} \right) \\ u\left( 1,t \right) = U\left( 1,t \right) = A + \sin\left( 1 + Ct \right) \\ \end{matrix}\end{split}\]

Note that in this example, the fixed (Dirichlet) boundary condition varies with time.

The type of boundary condition is insignificant to the method of manufactured solutions. One can easily choose Neumann (flux conditions at the boundary), Cauchy (a mix of fixed conditions and at least one derivative in the direction of the normal of the boundary), Robin (weighted combinations of Neumann and Dirichlet conditions over all boundaries) or mixed conditions (different boundary condition types on different subsets of the boundary) as each partial differential equation application is explored.

By example, a different solution to our proposed problem will occur if we shift to a mixed boundary condition such that:

(2.11)\[\begin{split}\begin{matrix} u\left( 0,t \right) = U\left( 0,t \right) = A + \sin\left( 0 + Ct \right) = A + \sin\left( \text{Ct} \right) \left( \text{Dirichlet} \right) \\ \frac{\partial}{\partial x}\left( u\left( 1,t \right) \right) = \frac{\partial}{\partial x}\left( U\left( 1,t \right) \right) = \frac{\partial}{\partial x}\left( A + \sin\left( 1 + Ct \right) \right) = \cos\left( 1 + Ct \right) \left( \text{Neumann} \right) \\ \end{matrix}\end{split}\]

In this way, the method of manufactured solutions allows the investigator to examine how the application of different boundary conditions affects the overall veracity of numerical approximations within the context of problems where solutions can be found through explicit hand calculation.

5. Theoretically, when a manufactured exact solution is known, computer algorithms applied to imitate that result should converge systematically toward exactness as the calculation space is ever more refined. Ideally, one might expect an eventual numerical result to differ from an exact solution by no more than \(\mathcal{O}\left( \mathrm{\text{machine\ epsilon}} \right)\). Of course, the theoretical threshold of solution quality varies widely from this value as there are few calculations that can be held to such a high standard. For example, computers estimate all transcendental functions with truncated power series on computers, regardless of what a programmer types into code, and these functions are inherently burdened with this approximation error.

   However, one can systematically refine a mesh and recalculate the solution to proposed problems in search of exactness. Once the arithmetic difference between the discretized solution and a manufactured solution remains constant, regardless of further mesh refinement, one has discovered the best numerical solution possible for a given code and a given problem. If the error between discretized solution and manufactured solution is acceptable by some standard, a code can be considered numerically verified. Note that this verification is limited to those code components invoked when setting up a MMS. As is the case for MFIX, most codes are far too complex to complete a full verification in a single MMS.

6. Global discretization error, \(\text{DE}_{\mathcal{l}}\) , is the arithmetic difference between the computer (approximate or discrete) evaluation of the manufactured solution to a by hand (exact) solution. The script \(\mathcal{l}\) is to remind the user of mesh \(\mathcal{l}\)evel.

   Rather than evaluate discretization error one cell at a time, one can further consider global discretization error through various mathematical norms. An \(L_{1}\)norm is an average absolute error over all cell locations \(\left( ijk = 1,\ldots,n \right)\) in a calculation represented through an absolute difference.

(2.12)\[L_{1}:\ \ \ \left\| \text{DE}_{\mathcal{l}} \right\|_{1} = \frac{\sum_{ijk = 1}^{n}\left| \text{DE}_{\mathcal{l,}\text{ijk}} \right|}{n}\]

An \(L_{2}\) norm is a root mean square error over all cell locations \(\left( ijk = 1,\ldots,n \right)\).

(2.13)\[L_{2}:\ \ \left\| \text{DE}_{\mathcal{l}} \right\|_{2} = \sqrt{\frac{\sum_{ijk = 1}^{n}\left| \text{DE}_{\mathcal{l,}\text{ijk}} \right|^{2}}{n}}\]

An \(L_{\infty}\) norm is the maximum error in any single cell location \(\left( ijk = 1,\ldots,n \right)\).

(2.14)\[L_{\infty} = \left\| \text{DE}_{\mathcal{l}} \right\|_{\infty} = \operatorname{}\left| \text{DE}_{\mathcal{l,}\text{ijk}} \right|\]

7. As mesh size, \(h\), changes, one collects the normed values of global discretization error and applies them to create an observed order, \(p\).

(2.15)\[p = \frac{\ln\left( \frac{\left\| \text{DE}_{\mathcal{l +}1} \right\|}{\left\| \text{DE}_{\mathcal{l}} \right\|} \right)}{\ln\left( \frac{h_{\mathcal{l +}1}}{h_{\mathcal{l}}} \right)} = \frac{\ln\left( \frac{\left\| \text{DE}_{\mathcal{l +}1} \right\|}{\left\| \text{DE}_{\mathcal{l}} \right\|} \right)}{\ln\left( r \right)}\]

In this notation, mesh level, \(\mathcal{l}\), is largest at the coarsest mesh, and smallest at the most refined mesh. One will also see the observed order formula where the ratio between two mesh sizes (as seen in the denominator of \(p\)) is called a mesh refinement factor, \(r\). Furthermore, the term grid size measure, \(\breve{h}\), is a ratio formed by comparing the number of divisions making up the finest mesh to the current mesh. Fig. 2.1 works to clarify these definitions within the context of observed order, and illustrates an observed order plot where \(r = 2\), between subsequent mesh levels. Note that the use of grid size measure eliminates the need for any units in graphical representations of observed order.

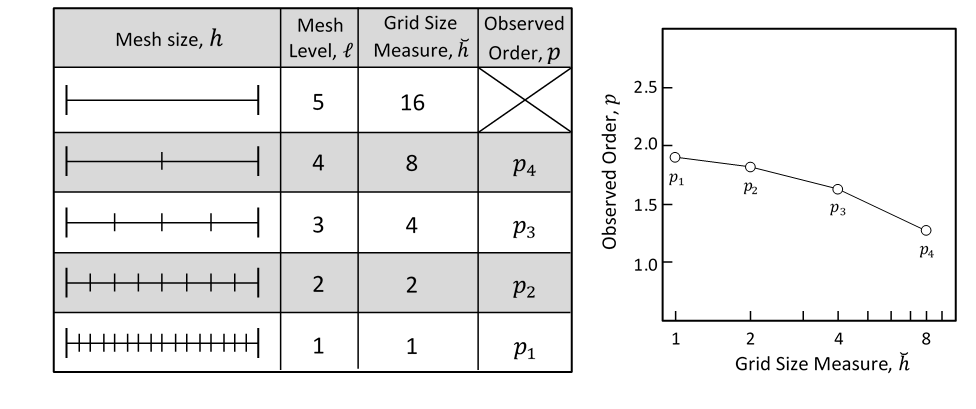
Fig. 2.1 Procedure for order of accuracy testing.

Ideally, one makes as many simulations as necessary to show that \(\operatorname{}p\) is constant, thereby inferring that the best possible numerical solution has been made, and further simulation is unwarranted.

Note that the norm chosen for the calculation of observed order may affect the outcome of this assessment. For example, the most challenging norm related above is \(L_{\infty}\), as it isolates the largest error in any given simulation. The least challenging norm is \(L_{1}\), as it will most easily mask localized high level error with areas of good agreement across any given domain.