2.10. MMS06: Pressure outflow BC, single-phase, 3D, curl-based functions

2.10.1. Description

The pressure outflow boundary condition in MFIX is verified using the techniques described in [5] where the manufactured solution is selected such that it satisfies both the divergence-free constraint and the pressure outflow condition. Specifically, this boundary condition requires that the pressure and all velocity components at the outflow have zero gradients normal to the wall at the boundary. For verification of the pressure outflow condition, the manufactured solution for the velocity field is given by Eq.2.48 while that for pressure is given by Eq.2.49 [6].

(2.48)\[\overrightarrow{V} = {\overrightarrow{V}}_{0} + S^{3}\left( \overrightarrow{\nabla} \times \overrightarrow{H} \right) + 3S^{2}\left( \nabla S \times \overrightarrow{H} \right)\]

(2.49)\[P = P_{0} + S^{2}P_{1}\]

Here, \(\overrightarrow{V}\) is the velocity field vector, \(S\) is the mathematical equation of the boundary tested (here, \(S \equiv y = 1\)), \(P_{0}\) is a non-zero scalar constant, \(P_{1}\) represents the sinusoidal terms of the general manufactured solution, and \(\overrightarrow{H}\) is a general vector field consisting of sinusoidal expressions.

2.10.2. Setup

This case is setup for single-phase flows on a domain with unit dimensions; the boundary tested is the North boundary (i.e., \(y = 1\)).

Table 2.18 MMS-06 Setup, Initial and Boundary Conditions.

Computational/Physical model
3D, Steady-state, incompressible
Single-phase (no solids)
No gravity
Turbulence equations are not solved (Laminar)
Non-uniform mesh
Central scheme
Geometry
Coordinate system	Cartesian
Domain length, \(L\) (x)	1.0	(m)
Domain height, \(H\) (y)	1.0	(m)
Domain width, \(W\) (z)	1.0	(m)
Material †
Fluid density, \(\rho_{g}\)	1.0	(kg·m-3)
Fluid viscosity, \(\mu_{g}\)	1.0	(Pa·s)
Initial Conditions
Pressure (gauge), \(P_{g}\)	0.0	(Pa)
Fluid x-velocity, \(u_{g}\)	5.0	(m·s-1)
Fluid y-velocity, \(v_{g}\)	5.0	(m·s-1)
Fluid z-velocity, \(w_{g}\)	5.0	(m·s-1)
Boundary Conditions ‡
North boundary	Pressure outflow
All other boundaries	Mass inflow (MMS)

† Material properties selected to ensure comparable contribution from convection and diffusion terms.

^‡ The manufactured solution is imposed on all boundaries (i.e., Dirichlet specification).

2.10.3. Results

Numerical solutions were obtained using the Central discretization scheme for 8x8, 16x16, 32x32, 64x64, and 128x128 grid meshes. The observed order of accuracy matches the formal order as shown in Figure 2‑15 for both the velocity variables and the pressure. Unlike the test cases verifying the no-slip and free-slip boundary conditions, no convergence issues were encountered since the problem has a physically-realistic outflow boundary.

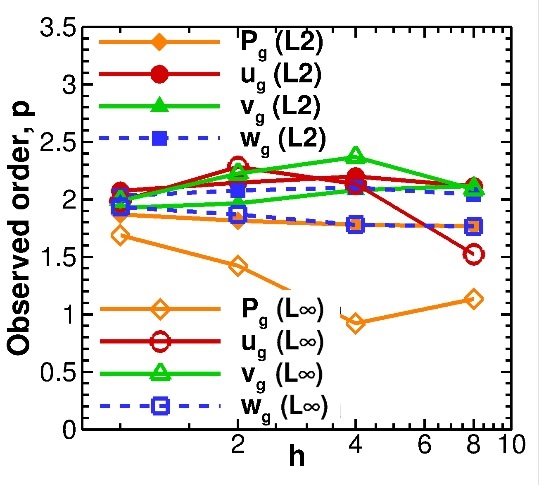
Fig. 2.18 Observed orders of accuracy for pressure outflow verification using \(\mathbf{L}_{\mathbf{2}}\) and \(\mathbf{L}_{\mathbf{\infty}}\) norms of the discretization error.